Algorithms Cache

Here are some algorithms I frequently use. Instead of putting them in some convoluted library, I simply look at them and re-implement them according to my data structures.

Simple sort for small arrays
Quick Sort
Removing duplicates from a sorted array
Binary Search
All Paths
Double Linked Dummy Head List
Bit Count
Highest set bit
Aligning an address to a power of two
Index of the lowest set bit
Sign of an Integer
Leap Years
Longest Common Substring
Rotating an Image by 90 Degrees

Simple sort for small arrays

sort(A,N):
   for i= 0 .. N-2
     for j= i+1 .. N-1 
       if A[i]>A[j]
          A[i] <-> A[j]

Quick Sort

qsort(A, left, right):
   if right <= left   done
   pos = left

   for i= left .. right
     if A[i] <= A[right]
        A[i] <-> A[pos]
        pos= pos+1

   A[pos] <-> A[right] 

   qsort(A, left, pos-1)
   qsort(A, pos+1, right)

This sort is recursive and requires a stack. However, it can be converted into a non-recursive algorithm by using a constant sized stack and converting the recursive calls into tail-recursive loops. In order to make sure that a constant size stack is sufficient, you need to push the left and right halves in a particular order.

If you push the bigger range first, you can always be sure that you won't need more than (N+1) stack positions if you have an N-bit machine (ie. 32 or 64). Our top-level algorithm will look like this:

RANGE= [0,N-1]
if RANGE is trivial, try to pop RANGE from stack. If the stack is empty, quit.
BIG,SMALL= partition(RANGE)
if BIG is not trivial, push it
RANGE= SMALL
goto step 2

It's easily seen that at each iteration of the loop, we're increasing the stack size by at most 1. Let B and S be the sizes of BIG and SMALL, respectively.

  B + S + 1 = N     ( one element is pivot and is not 
                      included  in neither BIG nor SMALL )
  B >= S
      add S+1 on both sides,
  B + S + 1 >= S + S + 1
      N >= 2S + 1
      S <= (N-1)/2

So, at each step, we're increasing the stack size by one but reducing the input size by more than half. This means that our stack usage F is:

  F(N) = F(N/2) + 1
  F(1) = 0
  F(N)= ceil(log2(N))

You can increase F(N) by one in order to push the smaller range as well. I also allocate a couple of more elements for the stack in case I make an off-by-one error or something. In any case, a constant-sized stack is enough for this. Just set the stack size to 70 and you'll be set for life:

  Assuming a 4Ghz processor and 1 store per cycle, we have:
   2^32 stores per second
  Filling up an array A with 2^69 elements in it would take:
   2^(69-32) = 2^37 seconds
             > 2^(37-6) minutes = 2^31 minutes  (64 second minute)
             > 2^(31-6) minutes = 2^25 hours    (64 minute hour)
             > 2^(25-5) days = 2^20 days        (32 hour day)
             > 2872 years
     2872*32/24*64/60*64/60= 4356 years

Removing duplicates from a sorted array

unify(A,N): 
  if N==0    done
  j= 0
  for i= 1 .. N-1
    if A[i]!=A[j]
       j= j+1
       A[j]= A[i]
  N= j+1

Binary Search

binary_search(A,N,key):
  i= 0
  j= N-1
  while i<=j
     k= (i+j)/2
     switch compare(key, A[k])
       >0 :  i= k+1
       <0 :  j= k-1
      ==0 :  return k
  end
  return -1

All Paths

A is an adjacency matrix:

all_paths(A, N):
  for k= 1..N
    for i= 1..N
      for j= 1..N
         A[i,j] |= A[i,k] & A[k,j]

This is also the basis for all-shortest-paths, where the |= operator is replaced by a conditional replacement.

Double Linked Dummy Head List

append(L,N):
  N->prev= L->prev
  N->next= L
  L->prev->next= N
  L->prev= N

prepend(L,N):
  N->next= L->next
  N->prev= L
  L->next->prev= N
  L->next= N

Highest set bit

uint8_t highestbit(uint8_t K)
{
  K |= K >> 1;
  K |= K >> 2;
  K |= K >> 4;
  return (K ^ (K>>1));
}

If K is abcdefgh, then the first OR makes it into

  a  b  c  d  e  f  g  h
| 0  a  b  c  d  e  f  g 
------------------------
  a ab bc cd de ef fg gh

the second one makes it

  a   ab   bc   cd   de   ef   fg   gh 
| 0    0    a   ab   bc   cd   de   ef 
--------------------------------------
  a   ab  abc abcd bcde cdef defg efgh

The third one

  a  ab  abc   abcd  bcde  cdef  defg  efgh
|                    a     ab    abc   abcd
-------------------------------------------
  a ab  abc  abcd  abcde abcdef abcdefg abcdefgh

As you can see, proceeding from left to right, if any bit is one, then the rest of the bits also become one.

  K= 0(N) 1(M)    we want to have 0(N) 1 0(M-1)

  S= K>>1         0(N) 0 1(M-1)

  R= K ^ S        0(N) 1 1(M-1)
                ^ 0(N) 0 1(M-1)
                -----------------
                  0(N) 1 0(M-1)

Aligning an address to a power of two

  align(K,size):
    V= size-1
    return (K+V)&~V

Here, we're only interested in the lower N bits of K, where 2^N=size. Let's assume that 0≤K<size. The higher bits don't matter to us.

If K is zero, then the expression also returns zero. Otherwise, the sum computes a value size+Z. Since Z is less than size, it's represented only by the bits 0..N-1. When we mask them out and only keep bit N.

Index of the lowest set bit

This function first finds the lowest set bit, just like highestbit above. It does this by shifting to the left instead of shifting to the right. However, the final masking isn't done, we simply leave a string of 1s at the top of the word.

After that, we invert the value and count the number of set bits.

  int one_index(uint64_t A)
  {
    uint32_t i,j;
    static const uint64_t B[]=
    {
      0x5555555555555555ll,
      0x3333333333333333ll,
      0x0f0f0f0f0f0f0f0fll,
      0x00ff00ff00ff00ffll,
      0x0000ffff0000ffffll,
      0x00000000ffffffffll
    };
  
    for(i=1;i<64;i<<=1) A |= (A<<i);
    A = ~A;
    for(j=0,i=1;i<64;i<<=1,j++) A= (A&B[j]) + ((A>>i)&B[j]);
    return A;
  }

When I compiled this with gcc -O3, it did an amazing job. It unrolled both loops and completely eliminated i,j and B. It also eliminated the last entry of B. Instead of masking the 64-bit register with 32 ones, it simply used eax.

When I changed the type of A to uint32_t, it again produced an almost optimal code for 32 bits, without changing anything else (it couldn't figure out that the last left shift of 32 bits was unnecessary). Simply amazing.

Finding the index of the highest set bit is almost identical, here is the code part only.

    for(i=1;i<64;i<<=1) A |= (A>>i);
    for(j=0,i=1;i<64;i<<=1,j++) A= (A&B[j]) + ((A>>i)&B[j]);
    return (A+64)%65;

The declarations are the same.

Sign of an Integer

  int sign(int x)
  {
    x|= x>>1;
    return ((unsigned)-x>>31) - ((unsigned)x>>31);
  }

It's funny that the "naive" implementation of this outperforms anything else, with gcc on amd64:

  int sign(int x) { return x<0 ? -1 : (x>0?1:0); }

Leap Years

I saw this on the Internet:

 isleap = year % 4 ? 
             false : 
             year % 100 ? 
                   true :  
                   year % 400 ? 
                        false : true;

Longest Common Substring

LCS(A[N], B[M]) -> (Sa, Sb, Len)

  var L[N+1,M+1] 
  L[0,x]= 0  L[x,0]= 0

  Len= 0

  for i = 0 .. N-1
    for j = 0 .. M-1
      if A[i] != B[j]
         L[i+1,j+1]= 0
      else
         K= L[i+1,j+1]= L[i,j] + 1
         if K > Len
            Len= K
            Sa= i - Len +1 
            Sb= j - Len +1 
         endif
       endif

Here, L[i+1,j+1] holds information regarding A[i] and B[j]. It's bigger than the arrays by one for each dimension in order to make the algorithm simpler for the case where i=0 or j=0.

Rotating an Image by 90 Degrees

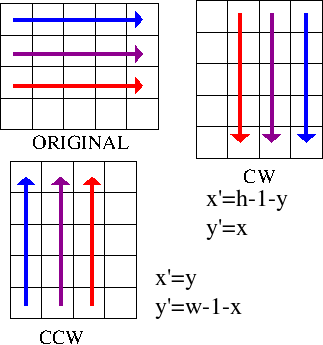
Bit Count

This is in fact part of the index of lowest set bit algorithm, but I forgot to record it. Counting set bits in an unsigned integer:

  A=  a₃a₂a₁a₀

     A & 0101b = 0a₂0a₀
+ A>>1 & 0101b = 0a₃0a₁
-----------------------
             B= c₁c₀d₁d₀

Here, cc is the count of the higher two bits and dd is the count of the lower two bits. We do the same thing, with a bigger width to combine cc and dd.

     B & 0011b = 00d₁d₀
+ B>>2 & 0011b = 00c₁c₀
-----------------------
             C = 0e₂e₁e₀
   is the count of the 4 bits.

We can continue like this to any width, combining elements by masking and adding. The list of shifts and masks are as follows:

The rest follows the same pattern. Here is the implementation for 32 bits:

int bit_count(uint32_t A)
{
  int i,j;
  unsigned int mask[5]=
  {
    0x55555555,
    0x33333333,
    0x0f0f0f0f,
    0x00ff00ff,
    0x0000ffff
  };
  for(i=0,j=1;i<5;i++,j<<=1)
    A= (A&mask[i]) + ((A>>j)&mask[i]);
  return A;
}

Here is a test program and its output:

I2luY2x1ZGUgPHN0ZGludC5oPgojaW5jbHVkZSA8dGltZS5oPgojaW5jbHVkZSA8c3RkbGli
Lmg+CiNpbmNsdWRlIDxzdGRpby5oPgoKc3RhdGljIGludCBiY19zaW1wbGUodWludDMyX3Qg
QSkKewogIGludCBpOwogIGludCBSOwogIGZvcihpPTAsUj0wO2k8MzI7aSsrKQogICBpZiAo
QSAmKDE8PGkpKSBSKys7CiAgcmV0dXJuIFI7Cn0KCmludCBiaXRfY291bnQodWludDMyX3Qg
QSkKewogIGludCBpLGo7CiAgdW5zaWduZWQgaW50IG1hc2tbNV09CiAgewogICAgMHg1NTU1
NTU1NSwKICAgIDB4MzMzMzMzMzMsCiAgICAweDBmMGYwZjBmLAogICAgMHgwMGZmMDBmZiwK
ICAgIDB4MDAwMGZmZmYKICB9OwogIGZvcihpPTAsaj0xO2k8NTtpKyssajw8PTEpCiAgICBB
PSAoQSZtYXNrW2ldKSArICgoQT4+aikmbWFza1tpXSk7CiAgcmV0dXJuIEE7Cn0KCnZvaWQg
cHJpbnRfYmluKHVpbnQzMl90IEspCnsKICBpbnQgaTsKICBmb3IoaT0zMTtpPj0wO2ktLSkK
ICB7CiAgIGlmIChpIT0zMSAmJiBpJTQ9PTMpIHByaW50ZigiXyIpOwogICBwcmludGYoIiVj
IiwgSyYoMTw8aSkgPyAnMSc6JzAnKTsKICB9Cn0KCmludCBwcmludF9zdGVwcyh1aW50MzJf
dCBBKQp7CiAgaW50IGksajsKICB1bnNpZ25lZCBpbnQgbWFza1s1XT0KICB7CiAgICAweDU1
NTU1NTU1LAogICAgMHgzMzMzMzMzMywKICAgIDB4MGYwZjBmMGYsCiAgICAweDAwZmYwMGZm
LAogICAgMHgwMDAwZmZmZgogIH07CiAgICBwcmludGYoIiAgaW5pdDogIik7IHByaW50X2Jp
bihBKTsgcHJpbnRmKCJcbiIpOwogIGZvcihpPTAsaj0xO2k8NTtpKyssajw8PTEpCiAgewog
ICAgQT0gKEEmbWFza1tpXSkgKyAoKEE+PmopJm1hc2tbaV0pOwogICAgcHJpbnRmKCJzdGVw
ICVkOiAiLCBpKTsgcHJpbnRfYmluKEEpOyBwcmludGYoIlxuIik7CiAgfQogIHJldHVybiBB
Owp9CgppbnQgbWFpbihpbnQgYXJnYyxjaGFyICoqYXJndikKewogIGludCBpLFosWSxOOwog
IHVpbnQzMl90IEs7CiAgc3JhbmQodGltZShOVUxMKSk7CiAgaWYgKGFyZ3ZbMV1bMF0hPScw
JykgewogIE49IGF0b2koYXJndlsxXSk7CiAgZm9yKGk9MDtpPE47aSsrKQogICB7CiAgICAg
IEs9IHJhbmQoKTsKICAgICAgWj0gYml0X2NvdW50KEspOwogICAgICBZPSBiY19zaW1wbGUo
Syk7CiAgICAgIGlmIChaIT1ZKSAKICAgICAgewogICAgICAgIHByaW50ZigiYml0IGNvdW50
IGZvciAleCBpczogc2ltcGxlOiAlZCwgcGFyYWxsZWw6ICVkXG4iLCBLLCBZLCBaKTsgCiAg
ICAgICAgcHJpbnRfc3RlcHMoSyk7CiAgICAgICAgcmV0dXJuIDE7IAogICAgICB9CiAgIH0K
ICB9CiAgZWxzZQogIHsKICAgIEs9IHN0cnRvbChhcmd2WzFdLCAwLCAwKTsKICAgIFo9IGJp
dF9jb3VudChLKTsKICAgIFk9IGJjX3NpbXBsZShLKTsKICAgIHByaW50ZigiYml0IGNvdW50
IGZvciAleCBpczogc2ltcGxlOiAlZCwgcGFyYWxsZWw6ICVkXG4iLCBLLCBZLCBaKTsgCiAg
ICBwcmludF9zdGVwcyhLKTsKICB9CiAgcmV0dXJuIDA7Cn0K

Testing:

bit count for 3c9e19c4 is: simple: 15, parallel: 15
  init: 0011_1100_1001_1110_0001_1001_1100_0100
step 0: 0010_1000_0101_1001_0001_0101_1000_0100
step 1: 0010_0010_0010_0011_0001_0010_0010_0001
step 2: 0000_0100_0000_0101_0000_0011_0000_0011
step 3: 0000_0000_0000_1001_0000_0000_0000_0110
step 4: 0000_0000_0000_0000_0000_0000_0000_1111