AVL Trees

AVL trees are a kind of balanced binary trees. Insertion and deletion from the tree is done like in a normal binary tree, but the operations are followed by a special rebalance operation.

The balance of the tree is kept by storing the height of each node and comparing left and right childrens' heights to determine whether a rotation is necessary or not.

A rotation is necessary when the height difference between the two childs of a node is greater than 1. For instance, if the left child of a node is 6 links high and the right child is 4 links high, then we can make a new subtree by rotating the subtree to right, resulting in two 5-high children. This operation is illustrated below:

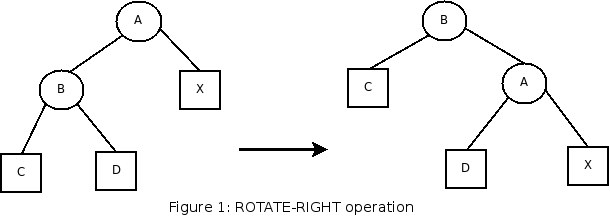
In this illustration, letters in circles denote single nodes and letters in boxes denote subtrees, which can possibly be null.

This operation by itself is not enough to maintain a balance in all cases, though. Consider the following situation:

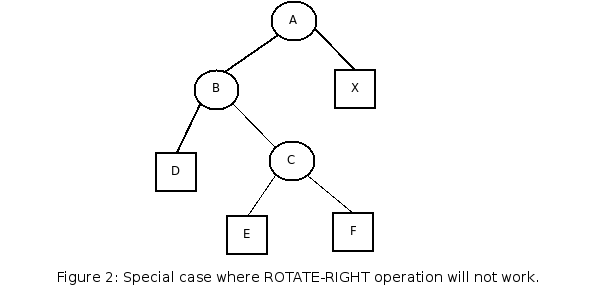
This case can be achieved by, for instance, inserting E when F was null. Making a right rotation in this case will not re-balance the tree at all:

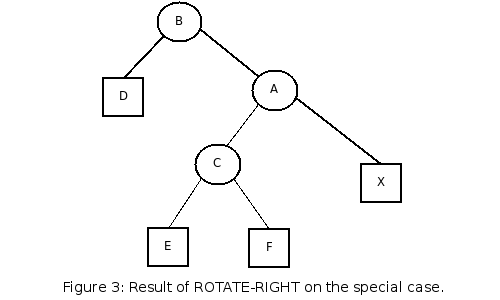
The operation has simply unbalanced the tree in the other direction. When we encounter such situations, we instead do the following:

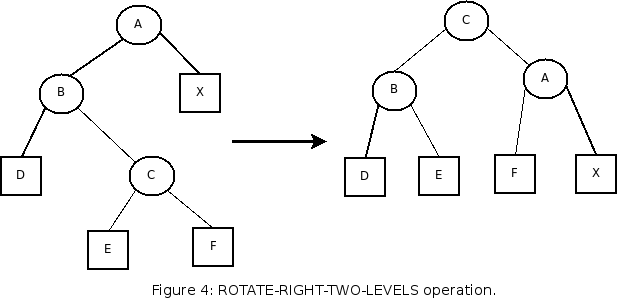
Choosing between a ROTATE-RIGHT and ROTATE-RIGHT-TWO-LEVELS is done by looking at the children of B. If B is left-heavy, then a ROTATE-RIGHT will not cause a new unbalance because the right child of B is not higher than the left child (see FIGURE 1). If B is right-heavy, then a ROTATE-RIGHT-TWO-LEVELS is necessary. The REBALANCE operation simply calculates the height of a node after an insertion or deletion, and then does the rotations, if any.

  REBALANCE (A):
    calculate_height (A);
    P= parent of A.
    U= height( A.left ) - height( A.right )
    if (U<-1)
       if left_heavy(A.right)
            rotate_left_twolevels(A)
       else
            rotate_left(A)
    else if (U>1)
        if right_heavy(A.left)
            rotate_right_twolevels(A)
        else
            rotate_right(A)
    rebalance(P);

As you can see, REBALANCE works up to the top of the tree.

    -[ c library "avl.c", header "avl.h" ]
    -[public] typedef struct anode {
        struct anode *left, *right, *parent;
        int height;
        int data;
    } anode_t;
    -[public] typedef struct {
        anode_t *root;
    } atree_t;
    -[public] void atree_insert (atree_t * T, int data)
    {
        node_t *N;
        anode_t *P;
        N = calloc (1, sizeof (*N));
        N->data = data;
        N->height = 1;
        if (!T->root)
        {
            T->root = N;
            return;
        }
        P = T->root;
        while (1)
        {
            if (N->data < P->data)
            {
                if (P->left)
                    P = P->left;
                else
                {
                    P->left = N;
                    N->parent = P;
                    break;
                }
            }
            else if (N->data > P->data)
            {
                if (P->right)
                    P = P->right;
                else
                {
                    P->right = N;
                    N->parent = P;
                    break;
                }
            }
            else
            {
                free (N);
                return;
            }
        }
        rebalance (T, N);
    }
    -[private] void calculate_height (anode_t * N)
    {
        int L, R;
        L = theight (N->left);
        R = theight (N->right);
        if (L > R)
            N->height = L + 1;
        else
            N->height = R + 1;
    }
    -[private] void rebalance (atree_t * T, anode_t * N)
    {
        int u;
        anode_t *P;
        calculate_height (N);
        u = theight (N->left) - theight (N->right);
        P = N->parent;
        if (u < -1) {
            if (left_heavy (N->right))
                rotate_left_twolevels (T, N);
            else
                rotate_left (T, N);
        } else if (u > 1) {
            if (right_heavy (N->left))
                rotate_right_twolevels (T, N);
            else
                rotate_right (T, N);
        }
        if (P)
            rebalance (T, P);
    }
    -[private] void replace_child_in_parent
        (atree_t * T, anode_t * old, anode_t * nw)
    {
        if (old->parent) {
            if (old->parent->left == old)
                old->parent->left = nw;
            else
                old->parent->right = nw;
        } else {
            T->root = nw;
        }
    }
    -[private] void rotate_right
         (atree_t * T, anode_t * A)
    {
        anode_t *B;
        B = A->left;
        A->left = B->right;
        if (A->left)
        A->left->parent = A;
        B->parent = A->parent;
        replace_child_in_parent (T, A, B);
        B->right = A;
        A->parent = B;
        calculate_height (A);
        calculate_height (B);
    }
    -[private] void rotate_right_twolevels
        (atree_t * T, anode_t * A)
    {
        anode_t *B, *C;
        B = A->left;
        C = B->right;
        /* we know that B and C are non-null since
        A was left heavy and B was right heavy */
        A->left = C->right;
        if (A->left)
            A->left->parent = A;
        B->right = C->left;
        if (B->right)
            B->right->parent = B;
        C->parent = A->parent;
        replace_child_in_parent (T, A, C);
        C->left = B;
        C->right = A;
        A->parent = C;
        B->parent = C;
        calculate_height (A);
        calculate_height (B);
        calculate_height (C);
    }
    -[private] int right_heavy (anode_t * A)
    {
        if (!A) return 0;
        return (theight (A->right) - theight (A->left)) > 0;
    }
    -[private] void
    rotate_left (atree_t * T, anode_t * A)
    {
        anode_t *B;
        B = A->right;
        A->right = B->left;
        if (A->right)
            A->right->parent = A;
        B->parent = A->parent;
        replace_child_in_parent (T, A, B);
        B->left = A;
        A->parent = B;
        calculate_height (A);
        calculate_height (B);
    }
    -[private] void rotate_left_twolevels
        (atree_t * T, anode_t * A)
    {
        anode_t *B, *C;
        B = A->right;
        C = B->left;
        /* we know that B and C are non-null since
        A was right heavy and B was left heavy */
        A->right = C->left;
        if (A->right)
            A->right->parent = A;
        B->left = C->right;
        if (B->left)
            B->left->parent = B;
        C->parent = A->parent;
        replace_child_in_parent (T, A, C);
        C->right = B;
        C->left = A;
        A->parent = C;
        B->parent = C;
        calculate_height (A);
        calculate_height (B);
        calculate_height (C);
    }
    -[private] int
    left_heavy (anode_t * A)
    {
        if (!A) return 0;
        return (theight (A->left) - theight (A->right)) > 0;
    }
    -[private] int theight (anode_t * A)
    {
        if (A) return A->height;
        else return 0;
    }
    -[ headers, begin ]
    !stdlib
    -[ end ]