Connected Pixels

For my rover project, I need to find connected sets of pixels within an image. This can be easily done with the flood fill algorithm (FFA). However, FFA has some drawbacks. Let's look at it: 
flood_fill_pixel(P, set):
  if visited[P], return set
  visited[P]= 1, set+= P 
  for each ON neighbour K of P
     set= flood_fill_pixel(K,set)
  return set

flood_fill_partition(I):
  visited[∀P]= 0
  partitions= nil set of sets
  while find(P) st. I[P] is ON and visited[P]= 0
     partitions += flood_fill_pixel(P, ∅)
  return partitions
This is pretty much it. There are variations on it such as using a queue instead of the call stack, travelling along a row before recursing etc. They are all simple optimizations of the above.

FFA literally restarts at every found pixel. Since it doesn't store its history in a useful manner, it can't derive guidance from its history and ends up being a brute force algorithm.

I think I can do better than that for the general case, a little worse for the worst case. I have an idea for a fast sequential algorithm and an idea for a multi-pass parallel one. Let's see how it goes.

Problem Definition

The algorithm will take a black-and-white image T. A pixel in T is set if it's white. I could use a greyscale image as well and use some threshold to decide whether a pixel is set or not.

I will then return an image S. In this image, two pixels will have the same color if they are part of the same connected set in T. The pixels of S don't really have color, they each contain a number which identifies the set they belong to. Black pixels in T are mapped to set 0.

Polygon Filling Revisited

For each pixel I will maintain a "set number" in an array S. S[P] identifies which set pixel P belongs to. S[P] will be 0 for a black pixel, and nonzero otherwise.

I will scan the image row by row from top to bottom and from left to right as follows. For a white pixel, if one of the neighbouring pixels above is white, we copy its set number. We use leftmost white neighbour for this. If such a neighbour can not be found, we copy the set number of the left pixel if it's white. If this also fails, we invent a brand new set number and use that.

Let's consider the following image. In this representation white squares are OFF pixels while colored squares are ON pixels in the original image. Each color represents a different set number.

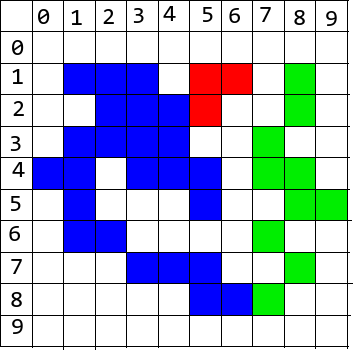
As you can see, this pass propagates colors from top to bottom, splitting at the joints when necessary. However, it can't combine two independent branches joining at the bottom. There are two of those in this example: blue-red joint at 24 and blue-green at 86. When we arrive at 24, we should somehow record the fact that blue and red sets are in fact one since 24 is a neighbour of both 13 and 15.

In order to achieve this, I will use an auxilliary array M. M[s] will hold a mapping from set number s to another set number z. If M[s]=z, then this will mean that all elements of s are also elements of z. M is initialized to M[s]=s.

Let's say blue=1, red=2 and green=3. When we reach 24, M looks like: 

  M[0]= 0  // set 0 is used for black pixels and not updated
  M[1]= 1
  M[2]= 2
  M[3]= 3
I will set M[2]= 1 and also S[15]= 1 (both blue). From now on, when I see a red square, I will understand that it's in fact a blue one. Setting S[15]=blue will also make S[25]=blue. However, this is not depicted on the image because it was constructed without this new strategy in mind. This modification is done only because we don't want further set joins caused by S[15] being red.

In order to avoid circular mappings, I will always set M[s]=z when z < s. If the values come out of this order, I will simply swap them.

When the scanning is done, it's time to flatten M. M basicly holds a forest of sets where each set points to its parent and the root of each tree points to itself. I can simply do the following: 

  for each s in M,
    while M[M[s]]!=M[s], M[s]= M[M[s]]
This simply updates the parent link of set s until it points to the root of the tree. After flattening, we can update S so that each pixel points to the root of its tree: 
  for each p in S, S[p]= M[S[p]]
If naming the sets in sequential numbers is desired, can have a parallel array N, which is created like so: 
  k= 1
  for each s in M, if M[s]==s, N[s]= k++
Then used as: 
  for each p in S, S[p]= N[M[S[p]]]

Memory Issues

Here, I have used two arrays for basic operation. S for output and M as auxilliary. Both of these arrays should be able to hold a set number in their elements. Maximum how many disjoint sets can we have in an image with dimensions WxH? The answer is WxH/4. In the worst case, each set would have only one element. In order to keep these lone pixels free of any white neighbours, we would have to have the same pattern over the whole image. For example: 
  . . . . . .
  . X . X . X
  . . . . . .
  . X . X . X
Any corner in a 2x2 block would work fine. For each group of 4 pixels, we can have only one white. This means that the number of isolated white pixels can be maximum a quarter of the total number of pixels. For a 640x480 image, this value is 76800. This is a manageable number. Having M this big won't be much of a problem. Since this doesn't fit in 16 bits, both M and S have to keep 32 bit elements. When you have 32 bit arrays, you can accomodate any image which fits in 4G (32 bit limit) since elements of M have two bits less than image size (WxH/4).

Now, if the input is 8 bit greyscale, M will be the same size as the input image. Its dimension is one fourth but each element is also four times bigger. So, the size comes equal. However, size of S will be four times the size of the input image. It has the same dimensions as the input image and four times the element size.

If memory is an issue, I could limit the number of sets. For example, I could limit it to fit in 16 bits. When I reach a certain threshold in sizeof(M), I could simply abort the whole thing and fall back to floodfill or something.

Implementation

To my surprise, it worked really nicely without too many problems on the first try. One issue was the proper joining of sets. I was thinking that simply setting M[a]=b would suffice for joining two sets. That was incorrect. This is because M[a] could have been updated before and when I set M[a]=b without checking, that relation gets lost. Now I walk both a and b to their roots and do the joinery there.

I think it's short enough to warrant a copy paste. Note that the input is 8 bit greyscale with threshold already applied. 

void joinset(uint32_t *M, uint32_t a, uint32_t b)
{
  while(M[a]!=a) a= M[a];
  while(M[b]!=b) b= M[b];

  if (a<b) { int t= a; a= b; b= t; }
  M[a]= b;
}

int scanfil(unsigned char *I, int W, int H, uint32_t **RS)
{
  uint32_t *M,*S,*N,R,A,B,C,L;
  M= malloc(sizeof(uint32_t)*(W*H/4+1));
  N= malloc(sizeof(uint32_t)*(W*H/4+1));
  S= calloc(W*H,sizeof(uint32_t));
  int i,x,y,K,lastset;
  M[0]= 0;
  lastset= 0;

#define input(x,y)  I[(x)+(y)*W]
#define output(x,y) S[(x)+(y)*W]

  for(y=0;y<H;y++)
   for(x=0;x<W;x++)
   {
     if (!input(x,y)) continue;
     A= B= C= L= 0;
     if (y!=0)
     {
       if (x!=0 && input(x-1,y-1)) A= output(x-1,y-1);
       if (input(x,y-1))  B= output(x, y-1);
       if (x!=W-1 && input(x+1,y-1)) C= output(x+1,y-1);
     }
     if (x!=0 && input(x-1,y)) L= output(x-1,y);

     if (A==0 && B==0 && C==0)
     {
       if (L==0)
       {
         K= ++lastset;
         output(x,y)= K;
         M[K]= K;
         continue;
       }
       output(x,y)= L;
       continue;
     }

     if (A==0) { if (B==0) R= C; else R= B; } else R= A;

     if (C!=0 && R!=C) { output(x+1,y-1)= R; joinset(M, C, R); }
     if (B!=0 && R!=B) { output(x, y-1)= R; joinset(M, B, R); }
     if (L!=0 && R!=L) { joinset(M, L, R); }
     output(x,y)= R;
   }

   for(i=1;i<=lastset;i++)
     while( M[M[i]]!=M[i] ) M[i]= M[M[i]];

   int la=1;
   N[0]= 0;
   for(i=1;i<=lastset;i++)
     if (M[i]==i) N[i]= la++;

   for(i=0;i<W*H;i++) S[i]= N[M[S[i]]];
   *RS= S;
   free(M); free(N);
   return la-1;
}
Here is a test program for it. It takes a PNG image argv[1], converts it to greyscale and thresholds it with value argv[2]. The image is then partitioned. Each partition is colored with a random color and the result is written to argv[3] as a PNG image. Here is an example run:

Optimizations

The above code is begging for optimization. There are so many things that could be done: This is just a big funpack waiting to happen.