Memory Requirement for Karatsuba Algorithm

Let's remember the algorithm from the parent page: 
R= A ⊗ B is      // R initially all zeros
  1:   if |A| < |B|  ⇒ A ⟷ B
  2:   if |B|=1      ⇒ R= A × B  .done.
  3:   M= ⌊|A|/2⌋
  4:   a1:a0 = A    s.t. |a1|= |A|-M, |a0|= M
  5:   if M ≥ |B| 
  6:      R = a0 ⊗ B
  7:      T((|a1|+|B|)) = a1 ⊗ B
  8:      R{M} += T
  9:      .done.
 10:   b1:b0 = B    s.t. |b1|= |B|-M, |b0|= M 
 11:   R= a0 ⊗ b0
 12:   R{2M}= a1 ⊗ b1
 13:   Sa,Ta = a0 ⊖ a1
 14:   Sb,Tb = b1 ⊖ b0
 15:   P((|Ta|+|Tb|))= Ta ⊗ Tb
 16:   mixed_sum(R, M) 
 17:   R{M} ⊕= Sa XOR Sb : P
We are now left with the following variables allocated at shown lines: I will initially ignore T, which is used in a small branch. This is because its memory requirement will be less than the main branch. Therefore, calculating the requirement for P+Ta+Tb will be enough.

There is no way to eliminate P, so we have to allocate some memory that. For Ta and Tb, we might get away with using the memory of a1 and b0, if we're allowed to modify our input. However, this isn't really an option because the recursive calls at (11) and (12) would mess up a0/1 and b0/1. Therefore, we're stuck with allocating memory for all variables listed above. Now let's look at how much memory we need for each variable.

For P, the answer is obvious from the code. It's |Ta|+|Tb|.

Ta is a difference of a0 and a1. Therefore, its length is the maximum of |a0| and |a1|. 

  |Ta| = max(|a0|,|a1|)
  |a1|= |a0|= M     , if |A| is even
  |a1|= |a0|+1= M+1,  if |A| is odd

  so, 
      |Ta|= |a1|= ceil(|A|/2)
Since |Tb|≤|Ta| (because |B|≤|A|), allocating the same space for it will also suffice.

So, the total requirement |P|+|Ta|+|Tb| is: 

  |P|= |Ta| + |Tb|
  Q= |P|+|Ta|+|Tb| = 2*(|Ta|+|Tb|)
  |Tb|≤|Ta|
  Q ≤ 4*|Ta|
If we allocate the maximum amount, 
  Q= 4*ceil(|A|/2)
   = 2*|A|     if  |A| is even,
   = 2*(|A|+1) if  |A| is odd
Now, notice that Q depends only on |A| since we made sure that B is shorter than A at the beginning. However, this won't be true all the time as we descend down the recursive call tree. At some point, |A| will get smaller than |B| and the value of |A| will increase. I will deal with this now. Let's call a and b the lengths of |A| and |B| in a particular call to our function. Then we have: 
  Q(a,b)= 4*ceil( max(a,b) / 2 )
Note that this memory is needed to execute the current call of the function and it doesn't include memory needed for the recursive calls.

Writing down the recursive formula is easy enough, but solving it isn't. So, I'm going to simply write some function that emulates ⊗ but only computes the necessary space instead of doing the actual computation. Maybe I can fit some polynomial to that.

Here is the code that does that: 

100: int kspace(int a, int b)
101: {
102:  int M,a0,b0,a1,b1,Ta,Tb, R;
103:  if (a<b) { int t; t=a; a=b; b=t; }
104:  if (b==1) return 0;
105:  M= a/2;         // = floor(a/2)
106:  a0= M; a1= a-M;
107:  if (b<=M) return a1+b + max2(kspace(a0,b), kspace(a1,b));
108:  b0= M; b1= b-M;
109:  Ta= max2(a1,a0);
110:  Tb= max2(b1,b0);
111:  R= max3(kspace(a0,b0), kspace(a1,b1), kspace(Ta,Tb));
112:  return R+ 2*(Ta+Tb);
113: }
This results in a value somewhere around 4*max(A,B), but the latter underestimates kspace(A,B). I wonder if I can simplify kspace and get some sort of a closed form. We know that 
  a1= ceil(a/2)
  a0= floor(a/2)
So, their maximum is a1. This can be replaced in (109). 
109:  Ta= max2(a1,a0);
109:  Ta= a1;
This makes Ta and its computation redundant. We also know that a0=b0=M due to (106) and (108). Let's replace all that: 
100: int kspace(int a, int b)
101: {
102:  int M,a1,b1,Tb, R;
103:  if (a<b) { int t; t=a; a=b; b=t; }
104:  if (b==1) return 0;
105:  M= a/2;         
106:  a1= a-M;
107:  if (b<=M) return a1+b + max2(kspace(M,b), kspace(a1,b)); 
108:  b1= b-M;
109:  Tb= max2(b1,M);
110:  R= max3(kspace(M,M), kspace(a1,b1), kspace(a1,Tb));
111:  return R+ 2*(a1+Tb);
112: }

A Simpler Subset

This function is too complicated to analyse by itself. Let's consider a simpler function G(x)= kspace(x,x). 
G(x)= kspace(x,x) : replace a and b by x.
202: int M,x1,x1,Tx, R;
203:  if (x<x) { int t; t=a; a=b; b=t; }
204:  if (x==1) return 0;
205:  M= x/2;         
206:  x1= x-M;
207:  if (x<=M) return a1+b+max2(kspace(M,b), kspace(a1,b)); 
208:  x1= x-M;
209:  Tx= max2(x1,M);
210:  R= max3(kspace(M,M), kspace(x1,x1), kspace(x1,Tx));
211:  return R+ 2*(a1+Tx);
We can see that the branches in (203) and (207) are never taken. (208) repeats the computation at (206). Computation of Tx is the same as the computation of Ta from before, so we have Tx=x1 again. Making these changes: 
200: int G(int x)
201: {
202:  int M,x1,R;
203:  if (x==1) return 0;
204:  M= x/2;         
205:  x1= x-M;
206:  R= max3(kspace(M,M), kspace(x1,x1), kspace(x1,x1));
207:  return R+ 2*(x1+x1);
208: }
Since all calls to kspace have symmetrical arguments, these can be replaced by G. Further simplifying (206) and (207), 
200: int G(int x)
201: {
202:  int M,x1,R;
203:  if (x==1) return 0;
204:  M= x/2;         
205:  x1= x-M;
206:  R= max2( G(M), G(x1) );
207:  return R+ 4*x1;
208: }
This becomes even easier if we split G into two parts, with even and odd x. 
200: int G(int x) { if (x%2) return G_odd(x); 
201:                    else return G_even(x); }
202: int G_even(x)
203: {
204:   int M,x1,R;
205:   if (x==1) return 0; // impossible x is even
206:   M= x/2;
207:   x1= x-M;
208:   R= max2(G(M), G(x1));
209:   return R+4*x1;
210: }
211:
212: int G_odd(x)
213: {
214:   int M,x1,R;
215:   if (x==1) return 0;
216:   M= x/2;
217:   x1= x-M;
218:   R= max2(G(M), G(x1));
219:   return R+4*x1;
220: }
For the even case, we can eliminate (205). Furthermore, we know that x1=M. Therefore, the max2 call at (208) also becomes useless. So, G_even becomes: 
202: int G_even(x)
203: {
204:   int M;
206:   M= x/2;
209:   return G(M)+4*M;
210: }
For the odd case, x1=M+1. Replacing this value into the function: 
212: int G_odd(x)
213: {
214:   int M,R;
215:   if (x==1) return 0;
216:   M= x/2;
218:   R= max2(G(M), G(M+1));
219:   return R+4*(M+1);
220: }
So, we have the following series: 
     G(1)=      0
    G(2M)=    G(M)            + 4*M        [1]
  G(2M+1)=  max(G(M), G(M+1)) + 4*M+4      [2]
If we calculate the difference [2]-[1], then we see that it's always positive. 
  G(2M+1)-G(2M)= max(G(M),G(M+1))+4M+4-G(M)-4M
               = max(G(M),G(M+1))-G(M)+4
     since max(G(M),X) ≥ G(M),    
  G(2M+1)-G(2M)> 0                      [A]
We can do a similar calculation for G(2M+2). 
  G(2M+2)= G(M+1) + 4 (M+1)= G(M+1)+4M+4   [3]
      subtracting [2] from [3],
  Δ(M)= G(2M+2)-G(2M+1)
           = G(M+1)+4M+4-max(G(M),G(M+1)-4M-4
           = G(M+1)-max(G(M),G(M+1))
           = G(M+1) + min(-G(M), -G(M+1))
           = min(G(M+1)-G(M), G(M+1)-G(M+1))
           = min(G(M+1)-G(M), 0)
Here, we have two cases, M can be odd or even. Let M=2k first, 
  Δ(M)=Δ(2k)= min( G(2k+1)-G(2k), 0)
        due to [A], G(2k+1) - G(2k) > 0
            = 0
Now let's set M=2k+1. 
  Δ(M)=Δ(2k+1)= min(G(2k+1+1)-G(2k+1), 0)
              = min(G(2k+2)-G(2k+1), 0)
              = min(Δ(k), 0)     (from definition of Δ(M))
Now we have the following: 
  Δ(M)= 0                 , even M
  Δ(M)= min(Δ((M-1)/2)),0), odd M
If we set m0=M, we can define the function as: 
  Δ(mi)= 0,              even mi
  Δ(mi)= min(Δ(mi+1),0), odd mi
  mi+1= (mi-1)/2
When we iterate this, eventually mi will become either 0 or an even number. This will result in an expression with a bunch of min() functions as zeros for arguments. The value of that expression will of course be 0. So we have shown that, for both odd and even M, Δ(M) is 0. Therefore, 
   G(2M+1) > G(2M)
   G(2M+2) = G(2M+1)
Which indicates a non-decreasing G. We can then remove the max operator from [2]: 
  G(2M+1)=  max(G(M), G(M+1)) + 4*M+4      [2]
  G(2M+1)=  G(M+1) + 4*M+4                 [2]
Replacing this in our original triple equations: 
     G(1)=      0
    G(2M)=    G(M) + 4*M                   [1]
  G(2M+1)=  G(M+1) + 4*M+4                 [2]
This can be rewritten with the ceiling function. 
  ceil((2M+1)/2)= M+1     ceil((2M)/2)= M

  G(1)= 0
  G(M)= G(ceil(M/2))+4*ceil(M/2)
This isn't a closed form, but log-time with regards to magnitude of M, which is pretty good. Let's try this: 
 int G(int x) {
    if (x==1) return 0;
    return G(CEIL(x,2)) + 4*CEIL(x,2);
  }
It does work pretty well. When I plot it against 4*x, there is very little difference. 4*x+60 exceeds G(x) up until 64K digits, so that's what I'm going to use. Here is the plot of G(x)-4x:

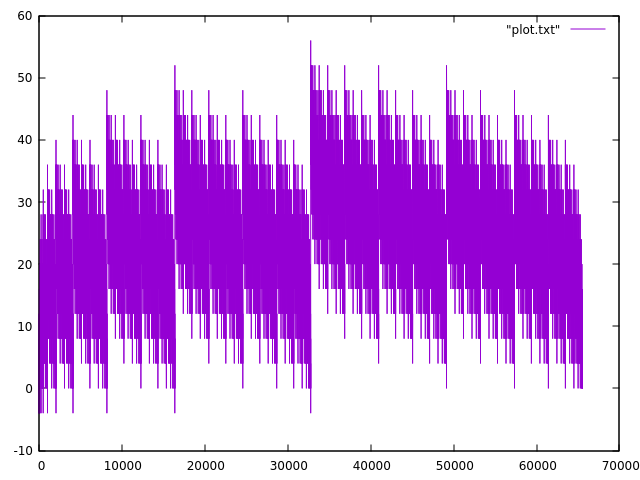
If you zoom in, the structure is self-repeating. It probably counts number of set bits or something. I mean look at this thing (G(x)-8*ceil(x,2)):

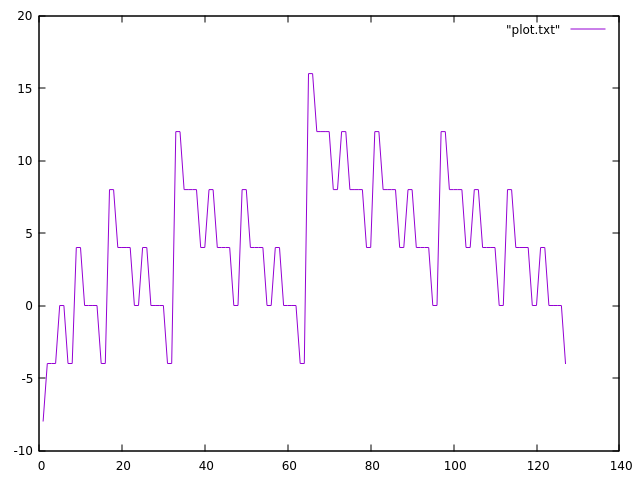
Anyway, the function f(x) defined as 
  f(x)=0,            x≤1
  f(x)=f(x/2)+2x+4,  x>1
overestimates G(x). Therefore, 4(x+ln(x)/ln(2)) is a good upper bound. If kspace(a,b) is increasing with regards to b, then G(a) is an upper bound on kspace(a,b) where b≤a. That's the only thing I need to prove from now on.

Another Subset

Another useful subset is kspace(x+1,x). This showed up in a couple of places while I was exploring for a closed form. 
200: P(X)= kspace(X+1,X) // let a= X+1, b= X
201: {
202:  int M,a1,b1,Tb, R;
203:  if (a<b) { int t; t=a; a=b; b=t; }
204:  if (b==1) return 0;
205:  M= a/2;         
206:  a1= a-M;
207:  if (b<=M) return a1+b + max2(kspace(M,b), kspace(a1,b)); 
208:  b1= b-M;
209:  Tb= max2(b1,M);
210:  R= max3(kspace(M,M), kspace(a1,b1), kspace(a1,Tb));
211:  return R+ 2*(a1+Tb);
212: }
We can immediately deduce that branches at (203) and (207) are never taken. Let's compute the rest of the numbers: 
200: P(x)= kspace(x+1,x) // let a= x+1, b= x
201: {
202:  int M,a1,b1,Tb, R;
204:  if (b==1) return 0; ⇒ if (x==1) return 0;
205:  M= a/2; ⇒ M=int((x+1)/2)=⌈x/2⌉
206:  a1= a-M; ⇒ a1=x+1-⌈x/2⌉=1+⌊x/2⌋
208:  b1= b-M; ⇒ b1=x-⌈x/2⌉=⌊x/2⌋
209:  Tb= max2(b1,M); ⇒ Tb=max2(⌈x/2⌉,⌊x/2⌋)=⌈x/2⌉
210:  R= max3(kspace(M,M), kspace(a1,b1), kspace(a1,Tb));
211:  return R+ 2*(a1+Tb);
212: }
Now we can get rid of all the variables and write this properly. 
P(1)= 0, 
P(x≠1)= max(kspace(⌈x/2⌉,⌈x/2⌉),
           kspace(1+⌊x/2⌋,⌊x/2⌋), 
           kspace(1+⌊x/2⌋,⌈x/2⌉))+ 2*(1+⌊x/2⌋+⌈x/2⌉)
The first call to kspace is in fact G(). The second one is a call to P(). I will let the third one stay as is for now. The final expression is just 2(1+x). 
P(1)= 0, 
P(x≠1)= max(G(⌈x/2⌉), P(⌊x/2⌋), kspace(1+⌊x/2⌋,⌈x/2⌉))+ 2x+2
The third term in the max function is actually redundant. 
 for even x, ⌈x/2⌉=⌊x/2⌋
  kspace(1+⌊x/2⌋,⌈x/2⌉)= kspace(1+⌊x/2⌋,⌊x/2⌋)= P(⌊x/2⌋)

 for odd x, ⌈x/2⌉=⌊x/2⌋+1
  kspace(1+⌊x/2⌋,⌈x/2⌉)= kspace(⌈x/2⌉,⌊x/2⌋)= G(⌈x/2⌉)
Both of these terms are already part of the max() expression. They can be removed safely. 
P(1)= 0, 
P(x≠1)= max(G(⌈x/2⌉), P(⌊x/2⌋))+ 2x+2
Let's compare this to G(x≠1). 
G(1)= 0
G(x)= G(⌈x/2⌉)+4⌈x/2⌉
P(x)-G(x)= max(G(⌈x/2⌉), P(⌊x/2⌋))+ 2x+2 - G(⌈x/2⌉)-4⌈x/2⌉
              = max(G(⌈x/2⌉), P(⌊x/2⌋))-G(⌈x/2⌉)+2x+2-4⌈x/2⌉
    since max(U,v) ≥ U, ⇒ max(U,v)-U≥0
P(x)-G(x) ≥ 0 + 2x+2-4⌈x/2⌉

for x=2k,
P(x)-G(x) ≥ 2(2k)+2-4⌈2k/2⌉= 4k+2-4k= 2

for x=2k+1,
P(x)-G(x) ≥ 2(2k+1)+2-4⌈(2k+1)/2⌉
P(x)-G(x) ≥ 4k+2+2-4(k+1)= 4k+4-4k-4=0
We can conclude two things from here:

Some Comparisons

While exploring the problem, I found the following difference to be of interest: 
λ(x)=G(x+1)-P(x)= K(x+1,x+1)-K(x+1,x)
This can be computed easily if we write down the formulas for P and G separately for odd and even cases. 
P(1)= 0, 
P(x≠1)= max(G(⌈x/2⌉), P(⌊x/2⌋))+ 2x+2
P(a=2k)= max(G(k),P(k))+2(2k)+2
P(a=2k)= P(k)+4k+2  // since P(x)≥G(x)
P(a=2k+1)= max(G(k+1),P(k))+ 2(2k+1)+2
P(a=2k+1)= max(G(k+1),P(k))+ 4k+4
G(1)= 0
G(a=2k)= G(k)+4k
G(a=2k+1)= G(k+1)+4k+4
We see that λ is defined recursively. 
λ(1)=G(2)-P(1)= 4-0= 4

λ(a=2k)= G(2k+1)-P(2k)= G(k+1)+4k+4-[P(k)+4k+2]
λ(a=2k)= 2+G(k+1)-P(k)= 2+λ(k)

λ(a=2k+1)= G(2k+2)-P(2k+1)
λ(a=2k+1)= G(k+1)+4(k+1)-[max(G(k+1),P(k))+4k+4]
λ(a=2k+1)= G(k+1)+4k+4-max(G(k+1),P(k))-4k-4
λ(a=2k+1)= G(k+1)-max(G(k+1),P(k))
λ(a=2k+1)= G(k+1)+min(-G(k+1),-P(k))
λ(a=2k+1)= min(G(k+1)-G(k+1),G(k+1)-P(k))
λ(a=2k+1)= min(0, λ(k))
It's easy to see that λ≥0. In fact, λ(x) is 0 for odd numbers (except for 1) and it counts the number of trailing zeros in binary for even numbers. 
λ(1)= 4
λ(2k+1)= 0
λ(2N)= 2N+4
λ(2N(2m+1))= 2N
Except for a few numbers, this is going to be much smaller than N, since it grows logarithmically. 
λ(1)= 4
λ(2)= 2.1+4= 6
λ(4)= 2.2+4= 8
λ(6)= 2.1= 2
λ(8)= 2.3+4= 10
λ(10)= 2.1= 2
λ(12)= 2.2= 4
λ(14)= 2.1= 2
λ(16)= 2.4+4= 12
After this point, λ(x)<x. Since λ≥0, the definition of P can be simplified a little bit: 
P(1)= 0
P(2k)= P(k)+4k+2
P(2k+1)= max(G(k+1),P(k))+4k+4
P(2k+1)= G(k+1)+4k+4= G(2k+1)
Let's look at yet another difference now: 
Φ(x)= G(x+1)-G(x)
I have strong hunch that this is also always non-negative. Remember G: 
G(1)= 0
G(2k)= G(k)+4k
G(2k+1)= G(k+1)+4k+4
Get on with it! 
Φ(1)= G(2)-G(1)= 4-0= 4

Φ(2k)= G(2k+1)-G(2k)
Φ(2k)= G(k+1)+4k+4-[G(k)+4k]
Φ(2k)= G(k+1)-G(k)+4k-4k+4
Φ(2k)= Φ(k)+4

Φ(2k+1)= G(2k+2)-G(2k+1)
Φ(2k+1)= G(k+1)+4(k+1)-[G(k+1)+4k+4]
Φ(2k+1)= G(k+1)+4k+4-G(k+1)-4k-4
Φ(2k+1)= 0
So, it was true. Let's summarize this section: 
λ(x)=G(x+1)-P(x) λ(1)=0 λ(2k+1)=0 λ(2k)=2+λ(k)
Φ(x)=G(x+1)-G(x) Φ(1)=0 Φ(2k+1)= 0 Φ(2k)=4+Φ(k)

Back to kspace

Let's recall the function to simplify it a little bit: 
100: int kspace(int a, int b)
101: {
102:  int M,a1,b1,Tb, R;
103:  if (a<b) { int t; t=a; a=b; b=t; }
104:  if (b==1) return 0;
105:  M= a/2;         
106:  a1= a-M;
107:  if (b<=M) return a1+b + max2(kspace(M,b), kspace(a1,b));
108:  b1= b-M;
109:  Tb= max2(b1,M);
110:  R= max3(kspace(M,M), kspace(a1,b1), kspace(a1,Tb));
111:  return R+ 2*(a1+Tb);
112: }
Here, if a≥b for the initial call to kspace, then it holds for all recursive calls. Therefore (103) can be done at a higher level, in the code which calls kspace/karatsuba.

In (107), we have two recursive calls:

We know that M≥b due to the condition at (107). Also, a1≥b because a1≥M (a1=⌈a/2⌉, M=⌊a/2⌋). In (110), we have the following recursive calls: Here, we know that a1≥b1 because a≥b. Also, a1≥Tb since a1≥M and a1≥b1. Since none of the recursive calls make b smaller than a, we can move (103) outside of kspace/karatsuba. We can also replace the call to kspace(M,M) with G(M). 
100: int kspace(int a, int b)
101: {
102:  int M,a1,b1,Tb, R;
103:  if (b==1) return 0;
104:  M= a/2;         
105:  a1= a-M;
106:  if (b<=M) return a1+b + max2(kspace(M,b), kspace(a1,b));
107:  b1= b-M;
108:  Tb= max2(b1,M);
109:  R= max3( G(M), kspace(a1,b1), kspace(a1,Tb));
110:  return R+ 2*(a1+Tb);
111: }
As before, we can split this function into two cases where a is even or odd. While we're doing that, we can also handle the case where a=b separately at the top level. 
int K(int a, int b)
{
  if (a==b) return G(a);
  else if (a%2) return Kodd(a,b);
       else return Keven(a,b);
}

Kodd(a=2k+1,b) // a>b, 2k+1>b, 2k≥b
{
  if (b==1) return 0;
  M= a/2 ⇒ M= k
  a1= a-M ⇒ a1= k+1
  if (b≤M)  return a1+b+max2(K(M,b), K(a1,b));
  b1= b-M ⇒ b1= b-k
  Tb= max2(b1,M) ⇒ Tb= max(b-k,k) ⇒ Tb=k (since b-k≤k)
  R= max(G(M), K(k+1,b-k), K(k+1,Tb))
  return R+2*(k+1+Tb);
}
Simplified further, replacing vars M,a1,b1,and Tb 
Kodd(a=2k+1,b) 
{
  if (b==1) return 0;
  if (b≤k)  return k+1+b+max2(K(k,b), K(k+1,b));
  return max(G(k), K(k+1,b-k), K(k+1,k))+2*(k+1+k);
}
Since K(k+1,k)= P(k): 
Kodd(a=2k+1,b) 
{
  if (b==1) return 0;
  if (b≤k)  return k+1+b+max2(K(k,b), K(k+1,b));
  return max(G(k), K(k+1,b-k), P(k))+2*(k+1+k);
}
Also, P(k)≥G(k), so the latter can be removed from the last line: 
Kodd(a=2k+1,b):
  b=1     ⇒ 0
  1<b≤k ⇒ k+1+b+max(K(k,b), K(k+1,b))
  k<b     ⇒ max(K(k+1,b-k), P(k))+4k+2
We can do the same things for Keven: 
Keven(a=2k, b) // a>b, 2k>b
{
  if (b==1) return 0;
  M= a/2 ⇒ M= k
  a1= a-M ⇒ a1= k
  if (b≤M) return a1+b+max2(K(M,b),K(a1,b))
  b1= b-M ⇒ b1= b-k
  Tb= max2(b1, M) ⇒ Tb= max(b-k,k) = k (since b-k<k)
  R= max3(G(M),K(a1,b1),K(a1,Tb))
  return R+2*(a1+Tb)
}
Replacing variables, a1=k, M=k, b1=b-k and Tb=k: 
Keven(a=2k, b) // a>b, 2k>b
{
  if (b==1) return 0;
  if (b≤k) return k+b+max2(K(k,b),K(k,b))
  return max3(G(k),K(k,b-k),K(k,k))+2*(k+k)
}
Since K(k,k)=G(k), we can remove it from the last max function. Also, the first max() call has two identical arguments. This call can be replaced with one of the arguments. 
Keven(a=2k, b):
  b=1     ⇒ 0
  1<b≤k ⇒ k+b+K(k,b) 
  k<b     ⇒ max(G(k),K(k,b-k))+4k
So, the final expression for K is: 
K(a,b)=
  a=b       ⇒ G(a)
  a=2k+1 ⇒ Kodd(a,b)
  a=2k      ⇒ Keven(a,b)
Kodd(a=2k+1,b):
  b=1     ⇒ 0
  1<b≤k ⇒ k+1+b+max(K(k,b), K(k+1,b))
  k<b     ⇒ max(K(k+1,b-k), P(k))+4k+2
Keven(a=2k, b):
  b=1     ⇒ 0
  1<b≤k ⇒ k+b+K(k,b) 
  k<b     ⇒ max(G(k),K(k,b-k))+4k

Increasing Function?

I have a hypothesis 
  G(a)≥K(a,b) ∀b≤a
To prove this, I can use yet another difference function 
δ(a,b)= G(a)-K(a,b)
δ(a,b)= 
G(a) -
{
  a=b       ⇒ G(a)
  a=2k+1 ⇒ Kodd(a,b)
  a=2k      ⇒ Keven(a,b)
}
δ(a,b)= 
  a=b       ⇒ G(a)-G(a)
  a=2k+1 ⇒ G(a)-Kodd(a,b)
  a=2k      ⇒ G(a)-Keven(a,b)
δ(a,b)= 
  a=b       ⇒ 0
  a=2k+1 ⇒ G(a)-Kodd(a,b)
  a=2k      ⇒ G(a)-Keven(a,b)
Let's handle the two cases separately. 
δ(2k+1,b)=G(2k+1)-Kodd(2k+1,b)
δ(2k+1,b)=
     G(2k+1)
        -
{
  b=1     ⇒ 0
  1<b≤k ⇒ k+1+b+max(K(k,b), K(k+1,b))
  k<b     ⇒ max(K(k+1,b-k), P(k))+4k+2
}
=
  b=1     ⇒ G(2k+1)-0
  1<b≤k ⇒ G(2k+1)-[k+1+b+max(K(k,b), K(k+1,b))]
  k<b     ⇒ G(2k+1)-[max(K(k+1,b-k), P(k))+4k+2]
       Replacing the value of G(2k+1)
=
  b=1     ⇒ G(k+1)+4k+4
  1<b≤k ⇒ G(k+1)+4k+4-k-1-b-max(K(k,b), K(k+1,b))
  k<b     ⇒ G(k+1)+4k+4-max(K(k+1,b-k), P(k))-4k-2
=
  b=1     ⇒ G(k+1)+4k+4
  1<b≤k ⇒ 3k+3-b+G(k+1)-max(K(k,b), K(k+1,b))
  k<b     ⇒ 2+G(k+1)-max(K(k+1,b-k), P(k))
       convert -max(u,v) to +min(-u,-v)
=
  b=1     ⇒ G(k+1)+4k+4
  1<b≤k ⇒ 3k+3-b+G(k+1)+min(-K(k,b),-K(k+1,b))
  k<b     ⇒ 2+G(k+1)+min(-K(k+1,b-k),-P(k))
       move G(k+1) inside min()
=
  b=1     ⇒ G(k+1)+4k+4
  1<b≤k ⇒ 3k+3-b+min(G(k+1)-K(k,b),G(k+1)-K(k+1,b))
  k<b     ⇒ 2+min(G(k+1)-K(k+1,b-k),G(k+1)-P(k))
       replace with known functions
=
  b=1     ⇒ G(k+1)+4k+4
  1<b≤k ⇒ 3k+3-b+min(G(k+1)-K(k,b),δ(k+1,b))
  k<b     ⇒ 2+min(δ(k+1,b-k),λ(k))
      rewrite G(k+1) in terms of G(k) and Φ(k)
=
  b=1     ⇒ G(k+1)+4k+4
  1<b≤k ⇒ 3k+3-b+min(Φ(k)+G(k)-K(k,b),δ(k+1,b))
  k<b     ⇒ 2+min(δ(k+1,b-k),λ(k))

δ(2k+1,b)=
  b=1     ⇒ G(k+1)+4k+4
  1<b≤k ⇒ 3k+3-b+min(Φ(k)+δ(k,b),δ(k+1,b))
  k<b     ⇒ 2+min(δ(k+1,b-k),λ(k))
We can do the same thing for δ(2k,b) 
δ(2k,b)= G(2k)-K(2k,b)
=
G(2k) -
{
  b=1     ⇒ 0
  1<b≤k ⇒ k+b+K(k,b) 
  k<b     ⇒ max(G(k),K(k,b-k))+4k
}
=
  b=1     ⇒ G(2k)-0
  1<b≤k ⇒ G(2k)-[k+b+K(k,b)]
  k<b     ⇒ G(2k)-[max(G(k),K(k,b-k))+4k]
         expand G(2k)
=
  b=1     ⇒ G(k)+4k
  1<b≤k ⇒ G(k)+4k-k-b-K(k,b)
  k<b     ⇒ G(k)+4k-max(G(k),K(k,b-k))-4k
=
  b=1     ⇒ G(k)+4k
  1<b≤k ⇒ 3k-b+G(k)-K(k,b)
  k<b     ⇒ G(k)-max(G(k),K(k,b-k))
            replace -max(u,v) with +min(-u,-v)
=
  b=1     ⇒ G(k)+4k
  1<b≤k ⇒ 3k-b+G(k)-K(k,b)
  k<b     ⇒ G(k)+min(-G(k),-K(k,b-k))
             move G(k) inside min()
=
  b=1     ⇒ G(k)+4k
  1<b≤k ⇒ 3k-b+G(k)-K(k,b)
  k<b     ⇒ min(G(k)-G(k),G(k)-K(k,b-k))
=
  b=1     ⇒ G(k)+4k
  1<b≤k ⇒ 3k-b+δ(k,b)
  k<b     ⇒ min(0,δ(k,b-k))
Let's summarize and also incorporate the case b=a into the two branches of δ 
δ(2k+1,b)=
  b=1		⇒ G(k+1)+4k+4
  1<b≤k		⇒ 3k+3-b+min(Φ(k)+δ(k,b),δ(k+1,b))
  k<b<2k+1	⇒ 2+min(δ(k+1,b-k),λ(k))
  b=2k+1	⇒ 0
δ(2k,b)=
  b=1		⇒ G(k)+4k
  1<b≤k		⇒ 3k-b+δ(k,b)
  k<b<2k	⇒ min(0,δ(k,b-k))
  b=2k		⇒ 0
It's easy to see that δ is never negative. 3k-b is always positive because it's only used in cases where b≤k. The other functions used G, λ and Φ are also non-negative. If we mark the non-negative parts above with ⋆ 
δ(2k+1,b)=
  b=1		⇒ ⋆
  1<b≤k		⇒ ⋆+min(⋆+δ(k,b),δ(k+1,b))
  k<b<2k+1	⇒ ⋆+min(δ(k+1,b-k),⋆)
  b=2k+1	⇒ 0
δ(2k,b)=
  b=1		⇒ ⋆
  1<b≤k		⇒ ⋆+δ(k,b)
  k<b<2k	⇒ min(0,δ(k,b-k))
  b=2k		⇒ 0
The recursion ends at b=2k or b=1, which are both non-negative. In the rest of the cases, we don't have any negative constants and we never subtract a value computed recursively. Therefore, δ can never go below zero. So, this concludes that 
 G(a) ≥ K(a,b) ∀ b≤a
So, we can use G(a) as an upper bound for K(a,b), making life much more easier.