Computing the Neighbourhood of a Path

When drawing pictures, paths are a useful tool to define contours and areas. Rendering them is a non-trivial task, if you want to use pens with non-trivial widths or effects.

Drawing thick lines and curves is a solved problem. However, joining basic elements or doing things with the distance of a point to the path is not so easy using standard algorithms.

For this reason, I wanted to compute the N-neighbourhood of a path. Such a set consists of points whose distance to the path is not more than N pixel units.

Here, distance to a path means the minimal distance between the center of a pixel to centers of all pixels on the path.

The path is defined by a sequence of pixels with no gaps between them. ie. any two consecutive pixels on a path are direct neighbours.

First Approach

Scanning thru the image and computing the distance to path for each pixel is quite difficult, although promising.

A simpler approach is to scan thru the path and determine the distance from each pixel on the path to pixels within a circle of radius N. Here is our first algorithm.

neighbours(P, N):
  distmatrix: matrix w/size (P.w+2N,P.h+2N) filled with +∞ 
  for p ∈ P:
    for u ∈ circle(center=p, radius=N):
       d= dist(u,p)
       if d < distmatrix[u]:
          distmatrix[u]= d
  return distmatrix

Here, the comparison is necessary because any point of the image might be within the N-circle of many points on the path. We need the minimal value.

This can be sped up, we don't really need to compute the circle for each p. The circle and distances to each point in the circle are constant. We can compute that circle once and then simply do comparisons.

neighset(N):
  set= ∅
  ∀x,y ∈ [-N,N]:
    d= dist( (x,y), (0,0) )
    if d≤N: 
       set += (x,y,d)
  return set

apply(S, P, D):
  ∀(dx,dy,d) ∈ S:
    if d < D[P.x+dx,P.y+dy]:
      D[P.x+dx,P.y+dy]= d

neighbours(P, N):
  neigh= neighset(N)
  distmatrix: matrix w/size (P.w+2N,P.h+2N) filled with +∞ 
  for p ∈ P:
    apply(neigh, p, distmatrix)
  return distmatrix

This works as expected, but is quite wasteful. At each step, the algorithm checks many distances which can be deduced to be more than the value already on the matrix.

A Better Approach

For example, let's assume our path is moving straight up at one point. When we do the move, there really isn't any point in checking the points below our current point. They are all closer to the previous point in the path. Therefore, we need to cut them out from our inspection set.

There are 8 such moves, if we exclude duplicate points on the path. These are enumerated as follows:

         dx<0    dx=0    dx>0
  dy<0     0       1       2       enum number= sign(dx)+3sign(dy)+4
  dy=0     3       4       5
  dy>0     6       7       8

dx=dy=0 is still enumerated to make the code cleaner, but it will never show up in real world usage. An interesting characteristic of this enumeration is that two enums sum to 8 if they are opposites of each other.

Anyway, we can generate 9 sets to check for each kind of move. Here is a rendering of these sets: Set 4, which corresponds to no move, is still computed in order to provide a set for the first point on the path.

Using these sets, we can cut the running time in half:

neigh_incremental(N, dx, dy):
  set= ∅
  ∀x,y ∈ [ -N .. N ]:
    d0= dist( (x,y), (0,0) )
    d1= dist( (x-dx, y-dy), (0,0) )
    if d1≤N and d1<d0:
       set += (x, y, d1)
  return set

compute9(N):
  ∀dx,dy ∈ {-1, 0, 1}:
     k= dx+3dy+4
     neigh[k]= neigh_incremental(N, dx, dy) 
  return neigh

classify(pprev, p):
  return sign(p.x-pprev.x)+3sign(p.y-pprev.y)+4

neighbours9(P, N):
  neigh[]= compute9(N)
  distmatrix: matrix w/size (P.w+2N,P.h+2N) filled with +∞ 
  apply(neigh[4], P[0], distmatrix)
  for i ∈ [1..len(P)-1]
    k= classify(P[i-1], P[i])
    apply(neigh[k], P[i], distmatrix)
  return distmatrix

While this is much better, there is still room for improvement.

One Step Further

Let's assume that our path does two up moves (enum=1) in a row. This corresponds to two of these babies: As you can imagine, there is a lot of overlap, and most of the pixels are already closer to the second pixel in the sequence (the one that is on top of the other).

For the first pixel, it would suffice to check the points on the same horizontal line. The rest will be handled by the next pixel. Excluding the no-move case, there are 64 such possibilities. I've laid them out in a table of size 81. 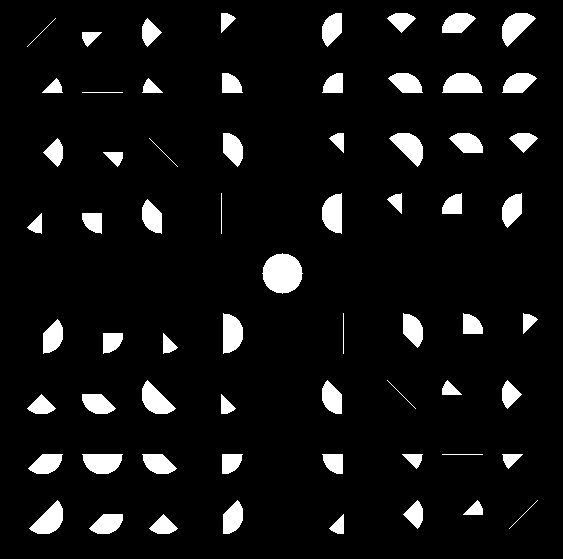Row 4 and column 4 are empty, since they will not be encountered in real world situations. I've put the full neighbourhood circle at position 40 in order to use it for the first and last pixels of the path.

As you can see, two identical moves cause the first move to check just a line of pixels, which is the absolute minimum. Following an up move with an up-right move causes an octant to be scanned. The only condition where you scan a full half circle is when you make the opposite move. ie. the path makes a down move immediately after an up move. This should be quite rare.

The code is similar to the previous iteration. It's just that we're now checking two moves instead of one.

neigh_incremental(N, dx1, dy1, dx2, dy2):
  set= ∅
  ∀x,y ∈ [ -N .. N ]:
    d0= dist( (x,y), (0,0) )
    d1= dist( (x-dx1, y-dy1), (0,0) )
    d2= dist( (x-dx1-dx2, y-dy1-dy2), (0,0) )
    if d1≤N and d1<d0 and d1<d2:
       set += (x, y, d1)
  return set

compute81(N):
  ∀dx1,dy1,dx2,dy2 ∈ {-1, 0, 1}:
     k= (dx1+3dy1+4)*9+(dx2+3dy2+4)
     neigh[k]= neigh_incremental(N, dx1, dy1, dx2, dy2) 
  return neigh

neighbours81(P, N):
  neigh[]= compute81(N)
  distmatrix: matrix w/size (P.w+2N,P.h+2N) filled with +∞ 
  apply(neigh[40], P[0], distmatrix)
  for i ∈ [1..len(P)-1)
    k= classify(P[i-1], P[i])*9+classify(P[i],P[i+1])
    apply(neigh[k], P[i], distmatrix)
  apply(neigh[40], P[len(P)-1], distmatrix)
  return distmatrix

Our code still runs at O(L.N²), where L is the length of the curve and N is the neighbourhood value. However, our average set size should be quite small compared to previous algorithms. In flat parts of the curve, it will converge to O(L.N).

Final Thoughts

Here is a rendering of the neighbourhood of a line, computed using this algorithm: The algorithm can't be improved further by adding another step of prediction. Third and subsequent moves don't add any valuable information.

As noted before, another approach is possible. We could paint the pixels of the path on an image and then propagate distance information out from the pixels, marking each processed pixel to avoid multiple checks for the same pixel. This has potential to be faster, but I'm happy with what I got so far.