Permutations
Applying a Permutation in Place
When you have a permutation, it's easy to apply it to an array if you're allowed to consume as much memory as the array itself. You just make a copy B and do B[i]= A[P[i]]. However, it's also possible to permute A directly, without creating a new array. Here I will construct an O(N) algorithm for doing this.Let us have N elements and a permutation array P. I will construct a list of exchange operations to be applied on the object array. The details of the object array are irrelevant since we're going to deal with only integer indices to this array and nothing else. We don't care about the element size, any offset into it or if it's actually an array or not.
void apply_permutation(int N, int *P, int *Rne, int **RE)
{
}
The returned values are in Rne and RE. The array (*RE) contains (*Rne)
pairs of integers, which are indices into the array. Elements at these
indices should be exchanged in order to permute the object array with P.
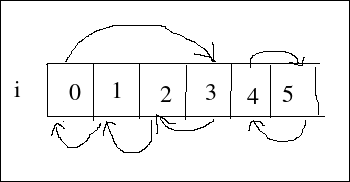
First of all, we should compute a target array T. T[i] holds which position the element at i will be moved to in order to achieve P. If we have a permutation like
N= 4
i 0 1 2 3
-----------
P= 1 2 3 0
the target array will be:
T= 3 0 1 2
A[0] should be moved to A[3], since P[3] = 0, T[0]= 3
A[1] should be moved to A[0], since P[0] = 1, T[1]= 0
A[2] should be moved to A[1], since P[1] = 2, T[2]= 1
A[3] should be moved to A[2], since P[2] = 3, T[3]= 2
Now, in order to compute T, we can simply loop on P[i] instead of T[i]. When
we see an element P[i]==k, we understand that element k will be put at position
i. This means that T[k]= i, implemented as follows:
int *T,i;
T= malloc(sizeof(int)*N);
for(i=0;i<N;i++)
T[P[i]]= i;
Permutation Cycles
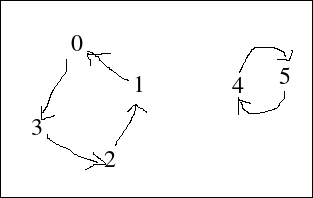
All permutations consist of disconnected cycles. Let's have a permutation P and its target array T. If you were to draw edges from i to T[i], you'd always end up with a set of disconnected cyclic graphs. Let's do this for the following permutation:P= 1 2 3 0 5 4 T= 3 0 1 2 5 4
This is quite hard for me to explain clearly, but it follows from the pigeonhole principle. Let's assume that we're copying from array A to array B in order to permute A with P. While doing this, we'll use T instead of P as follows:
- start walking T at an unvisited position, call this i0. i= i0
- store A[i] at B[T[i]]
- mark position i as visited
- i= T[i]
- continue from step 2, unless i is i0
- if there are any unvisited cells, restart from step 1.
In the fourth step, we move on to the next element in the assignment sequence. Now, T[i] can be one of two things:
- Option 1: A visited node
- Option 2: An unvisited node
If our case corresponds to option 2, we will expand the set of visited cells but we will face the same situation in the next iteration of the loop. Even if we always fall into option 2, eventually we will run out of unvisited nodes and go back to i0, which will complete a bigger cycle.
So, no matter which option is correct at a particular invocation of the
loop, eventually we will form cycles.
The above graph can be more explicitly drawn as:
Just think of it this way: every cell has to send its value to some other
cell and receive a value from some other cell. No two cells can send their
values to the same cell. When you draw the graph based on this, you
realize that this is a cycle because each node has exactly two edges.
The only possible configuration is a set of disjoint cycles.
In the above discussion, I omitted the trivial elements. If our permutation was
P= 1 2 3 0 5 4 6 T= 3 0 1 2 5 4 6The last element would not contribute to anything. It specifies that the last element of the object array must stay in place, so we don't touch it at all. When we draw this as a graph, we see that such elements form 1-node cycles with one edge for which the sending and receiving ends are at the single node.
So in general, if P[i]==i, we can ignore that node and continue processing.
Trivial Exchanges
Let's try to build our exchange list generator. I'll loop over T[i] and see what we can do. First of all, we can ignore i when T[i]==i.
int ne, *E;
E= malloc(sizeof(int)*N*2);
ne= 0;
for(i=0;i<N;i++)
{
if (T[i]==i) continue;
}
When we have a cycle with only two nodes in it, we're done with both nodes
after we make an exchange between them:
j= T[i];
if (T[j]==i)
{
E[ 2*ne ] = i;
E[ 2*ne+1] = j;
ne++;
T[i]= i;
T[j]= j;
continue;
}
When we make an exchange like this, we set T[j]= j so that we don't process
it again. j is always greater than i and we won't process element i again,
but I also set it to the trivial value just to be consistent.
Bigger Cycles
The above code leaves only cycles with more than two elements in them. When we encounter such cycles, we can simply reduce the number of nodes in it by one, until we reach a two-node cycle. As shown in the following diagram:
When we're processing element 0, we find out that it's not a trivial element and it's not part of a two-node cycle, so we decide to cut it out from the graph. We remove the node and its edges, but we introduce the new red edge from 1 to 3.
In order to do this, we first make an exchange between element 1 and element 0. After this, element 0 has gotten the correct value, but the old value in element 0 still has to go to element 3. Right now, it's stored in element 1 due to the exchange. So we update the graph and say that T[1]= 3. ie. send the 'new' value in element 1 to element 3.
So, we're cutting nodes now and we need to know the neighbours 1 and 3. Neighbour 3 is the next element in the cycle and can be trivially found in T[0]. How about element 1, the last element in the cycle?
In general, a cycle is represented as:
T[i0]== i1, T[i1]== i2, .. T[ik]== i0Let's assume that this is our very first node we're processing for this cycle. ie. T[i] has not been updated for any i in the cycle. We have to find out the value of ik.
T[P[i]]= i // initialization T[ik]== i // our constraint ik= P[i]So, it's right there in our faces. Just look at P[i] and you find the last node in the cycle. Which makes sense: P[i] holds the source node for the edge ending at node i and T[i] holds the destination node for the edge starting from i.
Now, for our assumption: after such an exchange we update T but not P. In our case, if we were to process element 3 after element 0, we would get the incorrect value from P[3] since it's still 0. Therefore, when we update T for this purpose, we should also update P. In the example above, processing element 0, we would set P[3]= 1. This now makes the equation
T[P[i]]== ian invariant, so our method for finding the last element of a cycle applies to all nodes, not just the first processed node in a cycle.
Summing it up, our processing code for big cycles is:
next= T[i]; prev= P[i]; E[2*ne] = i; E[2*ne+1]= prev; ne++; T[prev]= next; P[next]= prev;Here, I didn't set T[i]=i or P[i]= i since we're never going to reach index i: we've deleted all references to it. There were only two and they were in T[prev] and P[next].
Conclusion
I didn't expect this, but it turned out that we have to modify P. We could make a copy of it, but I'll leave it like this for now. This concludes our three cases, let's put them all together into one place.
void apply_permutation(int N, int *P, int *Rne, int **RE)
{
int *T,i,j,prev,next,*E,ne;
T= malloc(sizeof(int)*N);
for(i=0;i<N;i++)
T[P[i]]= i;
E= malloc(sizeof(int)*N*2);
ne= 0;
for(i=0;i<N;i++)
{
if (T[i]==i) continue;
j= T[i];
if (T[j]==i)
{
E[ 2*ne ] = i;
E[ 2*ne+1] = j;
ne++;
T[i]= i;
T[j]= j;
continue;
}
next= T[i];
prev= P[i];
E[2*ne] = i;
E[2*ne+1]= prev;
ne++;
T[prev]= next;
P[next]= prev;
}
*Rne= ne;
*RE= E;
free(T);
}
Now that I look at the whole function, two node cycles are just special
cases for big cycles where prev==next. So, I can remove that whole section
without affecting anything.
void apply_permutation(int N, int *P, int *Rne, int **RE)
{
int *T,i,prev,next,*E,ne;
T= malloc(sizeof(int)*N);
for(i=0;i<N;i++)
T[P[i]]= i;
E= malloc(sizeof(int)*N*2);
ne= 0;
for(i=0;i<N;i++)
{
if (T[i]==i) continue;
next= T[i];
prev= P[i];
E[2*ne] = i;
E[2*ne+1]= prev;
ne++;
T[prev]= next;
P[next]= prev;
}
*Rne= ne;
*RE= E;
free(T);
}
Here is a neat little application of the above algoritm. Instead of recording
the exchanges, I do it directly.
void permute(int N, int *_P, void *_A, size_t size)
{
int *T,*P,j,i,prev,next;
unsigned char *A,t;
T= malloc(sizeof(int)*N*2);
P= T+N;
A= (unsigned char*) _A;
for(i=0;i<N;i++)
{
P[i]= _P[i];
T[P[i]]= i;
}
for(i=0;i<N;i++)
{
if (T[i]==i) continue;
next= T[i];
prev= P[i];
for(j=0;j<size;j++)
{ t= A[i*size+j];
A[i*size+j]= A[prev*size+j];
A[prev*size+j]= t; }
T[prev]= next;
P[next]= prev;
}
free(T);
}
Inverse of a Permutation
I realized that the target array I computed above, T, could be the inverse of the original permutation P. Let's have an object array A and a permutation P. Permuting A by P is denoted as :A' = A perm PIf P' is the inverse of P, the following should hold:
A = (A perm P) perm P'It's actually quite simple. If you think of P as a network of cells as I mentioned above, in order to reach from A' to A again, you need to run the network backwards. i.e. you send the values from destinations to sources.
Our target array T and P define this network. For node i, T[i] is the destination node and P[i] is the source node. If you switch these around, the network will run in reverse and undo the effects of P on A. So, here is the inverse permutation function:
void inverse_permutation(int N,int *P, int **RI)
{
int *T,i;
T= malloc(sizeof(int)*N);
for(i=0;i<N;i++)
T[P[i]]= i;
*RI= T;
}
That was easy.
Associativity of Permutation
Is permutation associative?(A perm P) perm R == A perm (P perm R) ?Let's write a function which does P and R in the first order.
object_t* apply_composite(int N,object_t *A,int *P,int *R)
{
object_t *B, *C;
int i,j;
B= new_array(N);
C= new_array(N);
for(i=0;i<N;i++) B[i]= A[P[i]]; // 1
for(j=0;j<N;j++) C[j]= B[R[j]]; // 2
return C;
}
If r is the inverse (target array, as I called it before) of R, we
can write the second loop as:
for(j=0;j<N;j++) C[r[j]]= B[j]; // 3This means that, instead of looping on the permutation R and storing into C[] sequentially, loop on the target array r, read B sequentially and put each element of B into where it needs to go.
Now, both loops go thru B[] sequentially. This means that, when we have B[i] ready, we can immediately put it to the proper place according to R, but using r instead. So we can combine the loops like this:
for(i=0;i<N;i++) { B[i]= A[P[i]]; C[r[i]]= B[i]; } // 4
Now the array B is superfluous and can be removed.
for(i=0;i<N;i++) C[r[i]]= A[P[i]];We observe that sequential execution of the loop body is not necessary since all invocations of it are independent of each other. So, we can replace the loop index with anything at all, provided that we still cover all possible index values. i.e. we can do the C[r[i]]= A[P[i]] statements in any order. Let's use the order of R for this purpose:
for(i=0;i<N;i++) { j= R[i]; C[r[j]]= A[P[j]]; }
Here, at each invocation of the loop body, j gets a new value. We know that
it's different in each invocation since R is a permutation. So, replacing
j with its actual value, we get:
for(i=0;i<N;i++) C[r[R[i]]]= A[P[R[i]]];Since r and R are inverses of each other, r[R[i]]==i. This means that:
for(i=0;i<N;i++) C[i]= A[P[R[i]]];If you look at the indices of A in this loop, this is in fact permutation with Q where
Q = P perm R
Generating Permutations
There are well-known algorithms for generating all permutations. However, I'm not currently interested in those. I want to generate any given permutation, process it, and then convert the result back into a number. By iterating over the numbers 0 to N!-1, I could generate all permutations also. I'm doing this because I want to see how I can use permutations to understand sorting networks.Lexicographically Ordered
Let's go:
void gen_mth_perm(int M,int N,int *A)
{
int i,j,elt,idx;
static int fact[20];
if (!fact[0])
{ fact[0]= 1; for(i=1;i<20;i++) fact[i]= fact[i-1]*i; }
for(i=0;i<N;i++) A[i]= i;
for(i=0;i<N;i++)
{
idx= M / fact[N-i-1];
elt= A[idx+i];
for(j=idx+i;j>i;j--) A[j]= A[j-1];
A[i]= elt;
M %= fact[N-i-1];
}
}
This function takes O(N*N) time to generate a single permutation. It could
be made into a O(N*log(N)) function. In the above version, we store
unused elements
in array A. Since A needs to be kept sorted, all we can do is to shift
the elements around every time we remove an element from it. Instead of using
an array, we could use a tree-like structure to hold the unused elements in
sorted order. Then, we would have O(log(N)) time for element removal, which
would result in O(N*log(N)) time for the whole function. However, it's not
worth spending time where we're interested in all permutations
because N is going to be small anyway. I want to look into this later though.
For completeness sake, here is the inverse function, mapping from a permutation to its order.
int perm_number(int N,int *B)
{
int M,i,j;
M= 0;
for(i=0;i<N;i++)
{
M += B[i]*fact[N-i-1];
for(j=i+1;j<N;j++)
if (B[j]>B[i]) B[j]--;
}
return M;
}
Here, I simply modify the elements of B, which are larger than the last one
selected. This lets me reduce the amount of copying around. Let's see how
this works.
At each step, we're interested in the position of B[i] within the sorted array of the remaining unused numbers. We use this position to calculate the contribution of B[i] to M. During generation, the unused numbers were stored in A[i..N-1]. Let's name this part of A and call it U. Let's put this as the very first statement in the outer loop body in the generator:
U= A + i;When we shifted A[i..i+idx-1] to the right and increased i, something interesting happened. The indices of numbers greater than elt has decreased by one (with regard to U). Example:
i= 0
A= 0 1 2 3 4 5
U= 0 1 2 3 4 5 (U=A+0)
choose idx= 3 and continue to next step:
i= 1
A= 3 0 1 2 4 5
U= 0 1 2 4 5 (U=A+1)
Shifting the left part of U to the right and then increasing U by one
has the same effect as shifting the RIGHT part of U to the LEFT.
Now, all elements greater than A[i-1] have their indices decreased
by one. 4 is now in U[3]; it used to be in U[4] etc. Now, if we see
B[1]==4, we should use 3 as the factor since 4 is in the 3zix place.
In the inverse function I'm doing the same thing. When I see B[i], I add its contribution to M. After this, I decrement B[j] where B[j]>B[i] so that their indices in the updated U are calculated correctly.
This wasn't very clear but it's the best I can do. The code just popped into my head and it made perfect sense but explaining it clearly turns out to be quite difficult for some reason.
Not So Nicely Ordered
The above function generates lexicographically sorted permutations for increasing M. If this order is not necessary, it could be transformed into an O(N) function just by exchanging A[i] with A[idx+i] instead of shifting the array to keep it sorted. How I can find the order of a permutation generated like that is an interesting question. i.e. finding out M, given A. Let's do this. First, the modified permutation generation function:
void gen_mth_perm(int M,int N,int *A)
{
int i,j,elt,idx;
for(i=0;i<N;i++) A[i]= i;
for(i=0;i<N;i++)
{
idx= M / fact[N-i-1];
if (idx!=0)
{
elt= A[idx+i];
A[idx+i]= A[i];
A[i]= elt;
}
M %= fact[N-i-1];
}
}
This is almost identical to the one before, but we now have an exchange
operation instead of shift and store. The inverse function f(A)=M
turns out to be very similar to the generation function.
In order to find the number of a permutation, I thought maybe we can generate the permutation from scratch, and record our decisions about which element we chose at each step. After that, we can calculate the number using those decisions.
For this purpose, I will have an auxilliary array B, which serves as a placeholder for the generated permutation, which will be identical to the input when we're done.
Also, I will have an array called pos. In this array, I will store where each element lives. If pos[i]==k, then I will understand that element i is currently stored at position k in the array B. Here, by element I mean the actual integer value being permuted, not an index etc. For example:
index 0 1 2 3 4 5 B[0]= 0 => pos[0]= 0
----------- B[1]= 2 => pos[2]= 1
If B = 0 2 3 4 1 5 B[2]= 3 => pos[3]= 2
pos= 0 4 1 2 3 5 B[3]= 4 => pos[4]= 3
B[4]= 1 => pos[1]= 4
B[5]= 5 => pos[5]= 5
This looks awfully similar to an inverse permutation, but I'll look at it
later. Anyway, as I generate the target permutation by exchanging elements
in B, I'll update the pos array. For example, when I do an exchange
between B[i] and B[j], then the following will happen:
B[i] <-> B[j] => pos[B[j]]= i now that B[i] is stored at
pos[B[i]]= j position j and vice versa
I will walk thru the target permutation A and using A[i], I will choose
j such that A[i]==B[j]. This will let me reconstruct A within B, doing
the same exchanges I had done when constructing A. However, now I will
use j to compute the permutation number (previously, I had used the number
to determine j). So, the whole thing is
pretty straightforward:
int perm_number(int N,int *A)
{
int pos[20];
int B[20];
int T,i,j,M;
for(i=0;i<N;i++) pos[i]= B[i]= i;
M= 0;
for(i=0;i<N;i++)
{
j= pos[A[i]];
M+= (j - i)*fact[N-1-i];
pos[B[j]]= i;
pos[B[i]]= j;
T= B[i];
B[i]= B[j];
B[j]= T;
}
return M;
}
Now that I look at it again, pos is actually the inverse of B, since
pos[B[i]]==i. Hah.
Incrementally Generating All Permutations
There's a good algorithm for this, called Heap's Algorithm. I don't quite understand why it works, so I'm going to make my own using the last method. I think it's going to be equivalent in terms of time and space required.In my generation function, I have:
idx= M / fact[N-i-1];
A[i] <-> A[i+idx]
If I were to loop thru M, idx{i} would be zero for all values of i for
M=0. For M=1, it would be zero all the way and then 1 for the last
element. If I were to record idx somewhere, I could use it to generate
the next permutation quickly, without having to re-calculate most of
the idx values. I could just look them up from the array.
So I will do this:
- Look at the very last entry of idx: idx[N-2]. If it's not zero, restore the array to its previous configuration where the effect of idx[N-2] was not yet done.
- Increment idx[N-2]. If it is less than 2, then do the exchange and we're done.
- If idx[N-2] is 2, then it means that we've exhausted all permutations by changing only the last two elements. So, we should backtrack. Start from the first step, but using idx[N-3] instead. The backtrack value will now be 3.
- If you fail to goto step 1 above because we have already reached the very first element of idx[], then stop the algorithm: we've found all the permutations.
void init_incr_perm(int N,int *A,int *idx)
{
int i;
for(i=0;i<N;i++) { A[i]= i; idx[i]= 0; }
}
int incr_perm(int N,int *A,int *idx)
{
int p,i,t;
i= N-2;
p= 2;
again:
if (idx[i]!=0)
{
t= A[i];
A[i]= A[i+idx[i]];
A[i+idx[i]]= t;
}
idx[i]++;
if (idx[i]!=p)
{
t= A[i];
A[i]= A[i+idx[i]];
A[i+idx[i]]= t;
return 0;
}
idx[i]= 0;
i--;
p++;
if (i>=0) goto again;
return 1;
}
This function generates the permutations in the same order as I did
before, with the O(N) gen_mth_perm function.
Here is a test program for this:
I2luY2x1ZGUgPHN0ZGxpYi5oPgojaW5jbHVkZSA8c3RkaW8uaD4KCmludCBmYWN0Wz IwXTsKCmludCBleDsKCnZvaWQgZ2VuX210aF9wZXJtKGludCBNLGludCBOLGludCAq QSkKewogIGludCBpLGosZWx0LGlkeDsKCiAgZm9yKGk9MDtpPE47aSsrKSBBW2ldPS BpOwoKICBmb3IoaT0wO2k8TjtpKyspCiAgewogICAgaWR4PSBNIC8gZmFjdFtOLWkt MV07CiAgICBpZiAoaWR4IT0wKQogICAgewogICAgICBlbHQ9IEFbaWR4K2ldOwogIC AgICBBW2lkeCtpXT0gQVtpXTsKICAgICAgQVtpXT0gZWx0OwogICAgfQogICAgTSAl PSBmYWN0W04taS0xXTsKICB9Cn0KCgp2b2lkIGluaXRfaW5jcl9wZXJtKGludCBOLG ludCAqQSxpbnQgKmlkeCkKewogIGludCBpOwogIGZvcihpPTA7aTxOO2krKykgeyBB W2ldPSBpOyBpZHhbaV09IDA7IH0KfQoKaW50IGluY3JfcGVybShpbnQgTixpbnQgKk EsaW50ICppZHgpCnsKICBpbnQgcCxpLHQ7CiAgaT0gTi0yOwogIHA9IDI7CmFnYWlu OgogIGlmIChpZHhbaV0hPTApCiAgewogICBleCsrOwogICAgdD0gQVtpXTsKICAgIE FbaV09IEFbaStpZHhbaV1dOwogICAgQVtpK2lkeFtpXV09IHQ7CiAgfQogIGlkeFtp XSsrOwogIGlmIChpZHhbaV0hPXApCiAgewogICBleCsrOwogICAgdD0gQVtpXTsKIC AgIEFbaV09IEFbaStpZHhbaV1dOwogICAgQVtpK2lkeFtpXV09IHQ7CiAgICByZXR1 cm4gMDsKICB9CiAgaWR4W2ldPSAwOwogIGktLTsKICBwKys7CiAgaWYgKGk+PTApIG dvdG8gYWdhaW47CiAgcmV0dXJuIDE7Cn0KCmNoYXIgKnAyc3RyKGludCAqQSxpbnQg TikKewogIGNoYXIgKlI7CiAgaW50IGk7CiAgUj0gbWFsbG9jKE4rMSk7CiAgZm9yKG k9MDtpPE47aSsrKSBSW2ldPSBBW2ldKydhJzsKICBSW2ldPSAwOwogIHJldHVybiBS Owp9Cgp2b2lkIHBwZXJtKGludCBOLGludCAqQSkKewogIGludCBpOwogIGZvcihpPT A7aTxOO2krKykgcHJpbnRmKCIlYyIsQVtpXSsnYScpOwogIHByaW50ZigiXG4iKTsK fQoKaW50IHBhcnIoaW50IE4saW50ICpBKQp7CiAgaW50IGk7CiAgZm9yKGk9MDtpPE 47aSsrKSBwcmludGYoIiAlZCIsQVtpXSk7CiAgcHJpbnRmKCJcbiIpOwp9CgppbnQg bWFpbihpbnQgYXJnYyxjaGFyICoqYXJndikKewogIGludCBBWzIwXSxCWzIwXSxjb1 syMF07CiAgaW50IGksTjsKCiAgTj0gYXRvaShhcmd2WzFdKTsKICBmYWN0WzBdPSAx OwogIGZvcihpPTE7aTwyMDtpKyspIGZhY3RbaV09IGZhY3RbaS0xXSppOwogIAogIG luaXRfaW5jcl9wZXJtKE4sQixjbyk7CiNpZiAwCiAgZ2VuX210aF9wZXJtKDAsTixB KTsKCiAgZm9yKGk9MTtpPGZhY3RbTl07aSsrKQogIHsKICAgIGludCBqOwogICAgZm 9yKGo9MDtqPE47aisrKQogICAgICBpZiAoQVtqXSE9QltqXSkKICAgICAgewogICAg ICAgIHByaW50ZigiZmFpbGVkIGNoZWNrOiBBPSAlc1xuIgogICAgICAgICAgICAgIC AiICAgICAgICAgICAgICBCPSAlc1xuIiwgcDJzdHIoQSxOKSwgcDJzdHIoQixOKSk7 CiAgICAgIH0KICAgIGdlbl9tdGhfcGVybShpLE4sQSk7CiAgICBpbmNyX3Blcm0oTi wgQixjbyk7CiAgfQojZW5kaWYKCiAgZG8gCiAgICBwcGVybShOLEIpOwogIHdoaWxl KCFpbmNyX3Blcm0oTixCLGNvKSk7CgogIHByaW50ZigiZmluYWw9ICIpOyBwcGVybS hOLEIpOwogIHByaW50ZigiZmluYWxjbz0gIik7IHBhcnIoTixjbyk7CgogIHByaW50 ZigidG90YWwgbnVtYmVyIG9mIGV4Y2hhbmdlcz0gJWRcbiIsZXgpOwoKfQo=The test program shows that we make (N!*2-2) exchanges to generate all permutations, including the wraparound from the last permutation to the first one. Now that I've read Robert Sedgewick's presentation about the subject, I see that Heap's Algorithm takes only N! exchanges and my method here is just the backtracking algorithm. Now that I somewhat understand it, there is no easy path from this algorithm to Heap's Algorithm because the latter contains considerable effort on the structure of the problem. Mine is just depth-first search in disguise.
Heap's Algorithm
My backtracking algorithm is good enough for my purposes. Making 2N! exchanges is as good as N! exchanges because the time to process each permutation always takes much more time than doing an extra exchange, so the extra exchange is really insignificant. I just wanted to understand how Heap's Algorithm works.In his paper, Heap talks about the method but leaves substantial work to the reader. Namely, generating the tables.
The method goes like this:
- Choose one element and exchange it with what's at the end of the permutation.
- Recursively permute the rest of the elements, going thru all possible permutations.
- When you run out of sub permutations, goto step 1 using a different element this time.
N 2 0This means, after processing the trivial permutation, exchange elements 0 and 1. Now you have another permutation. The table is empty after that since now we got all the permutations. To process this properly, I will have a counter which holds the column number of the next exchange to be done. For N>=3, the counter will be an array, holding the column numbers for each row. This will basicly be an array counter similar to my backtracking algorithm.
Let's consider how this would work for N=3.
Start off with the trivial permutation: abc Now we use row 2 to permute the first two elements, after which we get bac We're done with all permutations with c at the end. Now let's put b at the end and see how we do. So, our first entry for row 3 is 0. cab Again doing the 2-perm: acb Now we will put a at the end. Again, our entry in the table is 0 since a occurs as the 0zix entry in the permutation. bca Do the 2-perm: cba Row 3 will be: 0 0Now our algorithm for calculating the rows will be as follows. Let k hold the symbol at the end of our permutation. We want to put k-1 at the end at the next step and its index will be the value we store in the table. We simply look at the permutation and find out where it is. We store that in the table and then run perm(N-1) so that the next step takes into account the effect of perm(N-1). I will call this effect of perm(N-1) the combined permutation or comper(N-1). This is simply the result when we run perm(N-1) on the string abcd...
comper(2) = 1 0 comper(3) = 2 1 0Let's find out row 4, after that I will write the function to do this.
perm= abcd
k= 'd'. Nothing to do here since we don't need an entry for the
first state, we just let it pass and prepare for the next
iteration.
now run comper(3)
perm= cbad
k= 'c'. position is 0. output this in the table.
do the exchange.
perm= dbac
run comper(3)
perm= abdc
k= 'b'. position is 1. output this in the table.
do the exchange.
perm= acdb
run comper(3)
perm= dcab
k= 'a'. position is 2. output this in the table.
do the exchange
perm= dcba
run comper(3)
perm= bcda
Here, the last permutation we got is actually comper(4). We went thru the
effect of all exchanges. At each step, we did some exchange to put the
desired element at the end and then run comper(3) to do the all exchanges
involving the first three elements. So, comper(4) comes for free in
this case:
comper(4)= 1230Here is the actual function which does this:
void compute_table_comper(int N) // the row in question
{
int col,i,t;
int sym;
int perm[20];
for(i=0;i<N;i++) perm[i]= i;
col= 0;
for(sym=N-2;sym>=0;sym--)
{
apply( perm, comper[N-1], N-1 );
for(i=0;i<N;i++) if (perm[i]==sym) break;
table[N][col++]= i;
t= perm[i];
perm[i]= perm[N-1];
perm[N-1]= t;
}
apply( perm, comper[N-1], N-1 );
for(i=0;i<N;i++) comper[N][i]= perm[i];
}
Here, sym starts off from N-2 because the whole set of numbers is [0,N-1].
No exchange is made for symbol N-1 because that's already at the end
for the initial condition in Heap's Algorithm.
Here is the output and the code for the test program:
N COMPER 2 1 0 3 2 1 0 4 1 2 3 0 5 2 3 4 1 0 6 1 2 3 4 5 0 7 2 3 4 5 6 1 0 8 1 6 3 2 5 4 7 0 9 2 7 4 3 6 5 8 1 0 10 1 2 3 4 5 6 7 8 9 0 11 2 3 4 5 6 7 8 9 10 1 0 12 1 6 3 8 5 10 7 2 9 4 11 0 N TABLE 2 0 3 0 0 4 0 1 2 5 2 0 2 0 6 2 3 2 1 2 7 4 2 0 4 2 0 8 4 1 6 1 0 1 2 9 6 0 4 4 2 2 6 0 10 6 7 0 5 4 3 8 1 2 11 8 6 4 2 0 8 6 4 2 0 12 8 5 2 9 8 3 2 7 8 1 2 I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRsaWIuaD4KCmludCB0YWJsZV syMF1bMjBdOwppbnQgY29tcGVyWzIwXVsyMF07Cgp2b2lkIGFwcGx5KGludCAqQSwg aW50ICpwZXJtLCBpbnQgTikKewogIGludCBUWzIwXSxpOwogIGZvcihpPTA7aTxOO2 krKykgVFtpXT0gQVtwZXJtW2ldXTsKICBmb3IoaT0wO2k8TjtpKyspIEFbaV09IFRb aV07Cn0KCnZvaWQgY29tcHV0ZV90YWJsZV9jb21wZXIoaW50IE4pIC8vIHRoZSByb3 cgaW4gcXVlc3Rpb24KewogIGludCBjb2wsaSx0OwogIGludCBzeW07CiAgaW50IHBl cm1bMjBdOwoKICBmb3IoaT0wO2k8TjtpKyspIHBlcm1baV09IGk7CiAgY29sPSAwOw oKICBmb3Ioc3ltPU4tMjtzeW0+PTA7c3ltLS0pCiAgewogICAgYXBwbHkoIHBlcm0s IGNvbXBlcltOLTFdLCBOLTEgKTsKCiAgICBmb3IoaT0wO2k8TjtpKyspIGlmIChwZX JtW2ldPT1zeW0pIGJyZWFrOwogICAgdGFibGVbTl1bY29sKytdPSBpOwoKICAgIHQ9 IHBlcm1baV07CiAgICBwZXJtW2ldPSBwZXJtW04tMV07CiAgICBwZXJtW04tMV09IH Q7CiAgfQogIGFwcGx5KCBwZXJtLCBjb21wZXJbTi0xXSwgTi0xICk7CiAgZm9yKGk9 MDtpPE47aSsrKSBjb21wZXJbTl1baV09IHBlcm1baV07Cn0KCnZvaWQgcHJpbnRfY2 9tcGVyKGludCBOKQp7CiAgaW50IGksajsKICBwcmludGYoIiAgTiBDT01QRVJcbiIp OwogIGZvcihpPTI7aTw9TjtpKyspCiAgewogICBwcmludGYoIiUzZCIsIGkpOwogIC Bmb3Ioaj0wO2o8aTtqKyspIHByaW50ZigiJTNkIiwgY29tcGVyW2ldW2pdKTsKICAg cHJpbnRmKCJcbiIpOwogIH0KfQoKdm9pZCBwcmludF90YWJsZShpbnQgTikKewogIG ludCBpLGo7CiAgcHJpbnRmKCIgIE4gRVhDSFxuIik7CiAgZm9yKGk9MjtpPD1OO2kr KykKICB7CiAgIHByaW50ZigiJTNkIiwgaSk7CiAgIGZvcihqPTA7ajxpLTE7aisrKS BwcmludGYoIiUzZCIsIHRhYmxlW2ldW2pdKTsKICAgcHJpbnRmKCJcbiIpOwogIH0K fQoKaW50IG1haW4oaW50IGFyZ2MsY2hhciAqKmFyZ3YpCnsKICBpbnQgaSxOOwogIE 49IGF0b2koYXJndlsxXSk7CiAgdGFibGVbMl1bMF09IDA7CiAgY29tcGVyWzJdWzBd PSAxOwogIGNvbXBlclsyXVsxXT0gMDsKICBmb3IoaT0yO2k8PU47aSsrKQogICAgY2 9tcHV0ZV90YWJsZV9jb21wZXIoaSk7CiAgcHJpbnRfY29tcGVyKE4pOwogIHByaW50 X3RhYmxlKE4pOwogIHJldHVybiAwOwoKfQo=The exchange list is exactly the same as Heap's as he presented in his paper. I just use 0-index where he uses 1-index.
If I change the order in which I put the elements at the end, I end up with slightly more interesting tables:
.. same ..
if (N%2) { start=0; step= 1; end= N-1; }
else { start=N-2; step= -1; end= -1; }
for(sym=start;sym!=end;sym+=step)
{
.. same ..
}
.. same ..
N COMPER
2 1 0
3 0 2 1
4 1 2 3 0
5 0 1 2 4 3
6 1 2 3 4 5 0
7 0 1 2 3 4 6 5
8 1 2 3 4 5 6 7 0
9 0 1 2 3 4 5 6 8 7
10 1 2 3 4 5 6 7 8 9 0
11 0 1 2 3 4 5 6 7 8 10 9
12 1 2 3 4 5 6 7 8 9 10 11 0
N TABLE
2 0
3 1 1
4 1 1 0
5 3 3 3 3
6 3 3 2 1 0
7 5 5 5 5 5 5
8 5 5 4 3 2 1 0
9 7 7 7 7 7 7 7 7
10 7 7 6 5 4 3 2 1 0
11 9 9 9 9 9 9 9 9 9 9
12 9 9 8 7 6 5 4 3 2 1 0
Here is the converse:
if (N%2==0) { start=0; step= 1; end= N-1; }
else { start=N-2; step= -1; end= -1; }
N COMPER
2 1 0
3 2 1 0
4 3 0 1 2
5 4 1 2 3 0
6 5 0 1 2 3 4
7 6 1 2 3 4 5 0
8 7 0 1 2 3 4 5 6
9 8 1 2 3 4 5 6 7 0
10 9 0 1 2 3 4 5 6 7 8
11 10 1 2 3 4 5 6 7 8 9 0
12 11 0 1 2 3 4 5 6 7 8 9 10
N TABLE
2 0
3 0 0
4 2 1 0
5 0 0 0 0
6 4 1 2 3 0
7 0 0 0 0 0 0
8 6 1 2 3 4 5 0
9 0 0 0 0 0 0 0 0
10 8 1 2 3 4 5 6 7 0
11 0 0 0 0 0 0 0 0 0 0
12 10 1 2 3 4 5 6 7 8 9 0
The order in which we choose the elements don't have to make sense
numerically. Basicly, we could choose any order between (N-1) elements.
The first element to go at the (N-1)zix position of the permutation
is always symbol (N-1). This is the initial condition from which we
start. We can't change that unless we initialize the permutation in
some other way. So, using a guide, we can decide on any order we
like:
void compute_table_comper(int N) // the row in question
{
int col,i,t;
char* sym;
int perm[20];
for(i=0;i<N;i++) perm[i]= i;
col= 0;
for(sym=guide[N];sym[0];sym++)
{
apply( perm, comper[N-1], N-1 );
for(i=0;i<N;i++) if (perm[i]==sym[0]-'a') break;
table[N][col++]= i;
t= perm[i];
perm[i]= perm[N-1];
perm[N-1]= t;
}
apply( perm, comper[N-1], N-1 );
for(i=0;i<N;i++) comper[N][i]= perm[i];
}
When I apply the guide from Heap's paper:
char *guide[]=
{
"", // 0
"", // 1
"a", // 2
"ba", // 3
"cba", // 4
"bcda", // 5
"ebcda", // 6
"dcbefa", // 7
"gbcdefa", // 8
"fedcbgha", // 9
"ibcdefgha", //10
"hgfedcbija", //11
"kbcdefghija",//12
};
The result is a nice table, which leads to the tableless Heap's Algorithm.
N COMPER 2 1 0 3 2 1 0 4 1 2 3 0 5 4 1 2 3 0 6 3 4 1 2 5 0 7 6 1 2 3 4 5 0 8 5 6 1 2 3 4 7 0 9 8 1 2 3 4 5 6 7 0 10 7 8 1 2 3 4 5 6 9 0 11 10 1 2 3 4 5 6 7 8 9 0 12 9 10 1 2 3 4 5 6 7 8 11 0 N TABLE 2 0 3 0 0 4 0 1 2 5 0 0 0 0 6 0 1 2 3 4 7 0 0 0 0 0 0 8 0 1 2 3 4 5 6 9 0 0 0 0 0 0 0 0 10 0 1 2 3 4 5 6 7 8 11 0 0 0 0 0 0 0 0 0 0 12 0 1 2 3 4 5 6 7 8 9 10So, given the guide, it's easy enough to come up with the algorithm. However, the reverse is more interesting. If we have the rules
- N is odd: table[N][i]= 0
- N is even: table[N][i]= i
Calculating Table Rows Using the Guide Array
It's much better to attack the problem from where I have come. i.e. given a valid guide[] entry, how do I find out the table[] row? Since all valid guide[] entries result in permutation generating algorithms (i.e. they never put the same symbol at the end twice), we're not concerned with the algorithm's correctness. All we care is how does the table[] and comper[] rows look like if we follow the pattern found in the above guide[] array.From now on, I shall use Sk to denote the symbols. It gets very confusing otherwise. S0=a, S1=b, .. etc.
We have the following patterns from what we know so far:
- For odd N:
- comper(N) = (N-1) 1 2 3 .. (N-2) 0
- table(N) = 0 0 .. 0
- guide(N) = SN-4 SN-5 SN-6 .. S1 SN-3 SN-2 S0
- For even N:
- comper(N)= (N-3) (N-2) 1 2 3 .. (N-4) (N-1) 0
- table(N) = 0 1 2 .. (N-2)
- guide(N) = SN-2 S1 S2 .. SN-3 S0
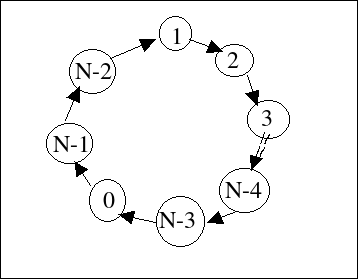
Here is the graph for comper(N):
I drew this graph using this algorithm:
i 0 1 2 3 4 .. N-3 N-2 N-1
comper (N-3) (N-2) 1 2 3 .. (N-4) (N-1) 0
comper[0]= N-3 edge from N-3 to 0
comper[1]= N-2 edge from N-2 to 1
comper[2]= 1 edge from 1 to 2
comper[3]= 2 edge from 2 to 3
..
comper[N-4]= N-5 edge from N-5 to N-4
comper[N-3]= N-4 edge from N-4 to N-3
comper[N-2]= N-1 edge from N-1 to N-2
comper[N-1]= 0 edge from 0 to N-1
When you straighten it out, it's obviously a single cycle.
Now that we're interested in table(N+1), let's look at guide(N+1). N+1 is odd, so:
- guide(N+1)= SN-3 SN-4 SN-5 .. S1 SN-2 SN-1 S0 [N entries in all]
- Initialize perm[i]= i for i in [0,N].
- For each entry u = guide[k], k ranging from 0 to N-2:
- Run comper(N) on perm[0..N-1]
- P= Find where u is in perm[0..N-1]
- Output P
- Exchange perm[P] with perm[N]
This concludes our proof that, if we obey the rules for generating guide(N+1), table[N+1] will be all zeros, given that our system works for all J ≤ N. However, there is one point remaining. Does comper[N+1] also follow our pattern??
Now I want to do the other half: Assume that our table generation algorithm works correctly for all J ≤ N where N is odd. Show that table(N+1)= 0 1 2 .. N-1.
I start in the same way, by drawing the graph of comper(N):
i 0 1 2 3 .. N-2 N-1
comper = (N-1) 1 2 3 .. (N-2) 0
By drawing edges from the numbers in the lower row to those
in the upper row, we get a much simpler graph, only the
first and last element get exchanged and everything else
stays in place.
If we look at guide(N+1), it will be obvious that this graph matches the guide and yields the rule table[N+1][i]=i.
- guide(N+1)= SN-1 S1 S2 .. SN-2 S0
Calculating the comper Array Using the Guide
In the previous section, I proved that the table[] would indeed follow the pattern we discovered if we abide by the rules for generating guide[]. However, I omitted the discussion of how comper[] would look like. This is necessary to complete the proof because I make use of the comper array in proving the former point.I have a hunch that finding out the inverse of comper(N) will be easier, by following where each symbol goes, making use of both guide(N) and comper(N-1).
Let's handle the case where N is even and N+1 is odd. I'm assuming that the guide rules yield comper rules for J ≤ N.
Now let's remember what we do for computing comper(N+1):
- Rotate the lower part 0..N-1 using comper(N)
- Exchange guide[i] (found at table[N][i]) with perm[N]
- Do the above steps for all elements of guide[]
- Do the rotation of the lower part once more.
Now let's see what happens to symbol SN. Initially, it's found in perm[N]. After the first rotation, it's exchanged into position 0 since all entries of table(N+1) are zero. After that, it never gets to position N, it continues its life within perm[0..N-1] according to comper(N). Now there are N rotations left ( we had N+1 total ). Symbol SN starts out from position 0 and then gets affected by N rotations of comper(N). It ends up at position 0.
So, comper(N+1)(0) = N.
Let's look at comper(N) again:

What happens to the symbol that got exchanged with SN? It follows
the same path SN did, but one it's one step behind. When THAT
one gets exchanged out of position N, the one following that also does the
same thing and on and on. How do we tell which symbol got exchanged with
SN? It's in the guide array. So, what happens is that, the
symbols in the guide array get lined up behind the position 0 according
to the above graph. Symbol SN is in position 0. S0
is in position N because it got exchanged into that position, but there
are no more elements in the guide(N+1) array to displace it. Summing it up:
- guide(N+1)= SN-3 SN-4 .. S1 SN-2 SN-1S0
perm[N-3]= guide(N+1)(0) = SN-3 perm[N-4]= guide(N+1)(1) = SN-4Now moving from the right end of guide(N+1) towards left, but skipping S0 since it doesn't get exchanged into perm[0..N-1]. We put these elements in positions we find by moving clockwise in the graph.
perm[N-1]= guide(N+1)(N-1)= SN-1 perm[N-2]= guide(N+1)(N-2)= SN-2 perm[1] = guide(N+1)(N-3)= S1 perm[2] = guide(N+1)(N-4)= S2We already have the following figured out:
perm[0]= SN perm[N]= S0If we put them together and sort them:
perm[0]= SN perm[1] = guide(N+1)(N-3)= S1 perm[2] = guide(N+1)(N-4)= S2 .. perm[N-4]= guide(N+1)(1) = SN-4 perm[N-3]= guide(N+1)(0) = SN-3 perm[N-2]= guide(N+1)(N-2)= SN-2 perm[N-1]= guide(N+1)(N-1)= SN-1 perm[N]= S0
- comper(N+1)= N 1 2 3 ... (N-1) 0
OK. Now N is odd and N+1 is even. We assume that our rules for generating guide(J) result in the pattern for comper(J) for J ≤ N. I need to show that comper(N+1) also follows the pattern we discovered. We have the following:
- comper(N) = (N-1) 1 2 3 .. (N-2) 0 [odd rule]
- table(N+1)= 0 1 2 .. (N-1) [even rule]
- guide(N+1) = SN-1 S1 S2 .. SN-2 S0 [even rule]
Let's look at what happens to symbol SN. Initially, it's at position N. After one execution of comper(N), it gets swapped out to position 0. Now, it will never go back to position N so it will get moved around according to comper(N) within perm[0..N-1]. As it was in the previous case, we have N executions of comper(N) left. N is odd, so SN will end up at position N-1 in the final perm[]. We got:
perm[N-1]= SN // 1After the first execution of comper(N), but before the first exchange, we have the following perm[] array:
perm = SN-1 S1 S2 .. SN-3 SN-2 S0 SNNow let's see what happens to symbols SN-1 to SN-3 in this sequence. At each step of comper(N+1) generation, we get an element according to table(N+1), swap it with perm[N], run comper(N) and in the next step we swap perm[N] with the next position in the table. Since the positions in the table are all sequential numbers, each element in the above sequence get shifted one cell to the right. For example:
- table[N+1][0]=0. so, get SN-1 (perm[0]) and exchange it with perm[N] (which currently has SN)
- we run comper(N)
- table[N+1][0]=1. so swap perm[N] (which now has SN-1) with perm[1].
perm[1]= SN-1 //2 perm[2]= S1 perm[3]= S2 .. perm[N-2]= SN-3When we are about to exchange element k of guide(N+1) with perm[N], we have made k+1 executions of comper(N). Before swapping guide(N+1)(0), we run it. After that we add one execution per element so we end up with k+1.
When we are about to swap SN-2 with perm[N], we have made N-1 executions of comper(N) since guide(N+1)(N-2)=SN-2:
- guide(N+1) = SN-1
S1
S2
..
SN-2
S0 [even rule]
guide(N+1) has N elements. Index of the last element is N-1. Index of SN-2 is N-2.
perm = S0 S1 S2 .. SN-3 SN-2 SN-1 SN // initial perm = SN-1 S1 S2 .. SN-3 SN-2 S0 SN // ran comper(N) once perm = SN S1 S2 .. SN-3 SN-2 S0 SN-1 // do the exchangeFrom this point on, neither perm[0] nor perm[N-1] gets exchanged with perm[N]. 0 was the first entry of table[], and we already did that. N-1 is near the end of table(N+1). So, these two positions contain S0 and SN from this point on, until we reach the last two elements of table(N+1).
Now, as I found out above, until we reach SN-2, we will have made N-1 executions of comper(N). After we did the initial execution of comper(N), we are left with N-2 executions. N-2 is an odd number. Therefore, perm[N-1] will contain SN and perm[0] will contain S0. Now, this is what perm[] looks like when we're about to exchange SN-2 with perm[N]:
perm= S0 SN-1 S1 S2 .. SN-2 SN SN-3Remember that we still haven't done the exchange which puts SN-3 into position N-2 as I had discussed before. We're about to do that. Let's proceed with the algorithm:
perm= S0 SN-1 S1 S2 .. SN-2 SN SN-3 // about to exchange
perm= S0 SN-1 S1 S2 .. SN-3 SN SN-2 // exchange done
perm= SN SN-1 S1 S2 .. SN-3 S0 SN-2 // ran comper(N)
perm= SN SN-1 S1 S2 .. SN-3 SN-2 S0 // last exchange
// between perm[N-1] <-> perm[N]
perm= SN-2 SN-1 S1 S2 .. SN-3 SN S0 // last execution of comper(N)
Since our permutation was initially perm[i]= Si, comper(N+1)
comes out as:
- comper(N+1)= (N-2) (N-1) 1 2 .. (N-3) N 0
Conclusion
So, what happened here? First, for small N, by inspecting the output of my program which uses the rules- table[even N]= 0 1 .. (N-1)
- table[odd N]= 0 0 ..
- guide[N]: the sequence of symbols to appear at the end of the permutation.
- comper[N]: the effect of generate(A,N) on array A=[0,1,2..N-1].
In the first part, I showed that if comper(N) is nice and guide(N+1) is nice, then table(N+1) is also nice.
In the second part, I showed that if comper(N), guide(N+1) and table(N+1) are nice, then comper(N+1) is also nice.
We already know that comper(N) and table(N) are nice for small N. guide(N+1) is always nice by definition: we generate it. So we conclude that table(N+1) is always nice.
Correctness of the algorithm follows from the way we generate guide[]. It never contains the same element twice, and never contains SN-1 (it's already there when we start the algorithm, so no selection is necessary to put it there). This means that each symbol gets to the end of the permutation exactly once and the rest of the array gets permuted with the remaining elements.
What I have proven is that if we follow the patterns for guide[], table[] will always follow the proposed rules.
Summary of the conclusion: Heap's Tableless Algorithm is correct because it's equivalent to Heap's Algorithm in which the table is created in a way that is guaranteed to result in a correct algorithm.
Notes
It's interesting to note that the generation algorithm and the table calculation algorithm are almost the same thing. The latter 'simulates' the former by using the comper[] array, which is the memoized result of generate(perm,N-1).I had done something similar when I was trying to get the permutation number of a given permutation. I had just simulated the situation where I was freshly generating the permutation and then used the decision variable to calculate the number instead of making a decision.