Subtracting Rectangles

Sometimes it's necessary to subtract rectangles in graphics operations. In my particular case, I had two sources of graphics (one OpenGL area and the rest was a bitmap) and I had to handle exposure events. I needed to divide the event rectangle in order to draw the OpenGL area and bitmap area independently, using different techniques.

As a first visualization of the problem, I came up with the following drawing:

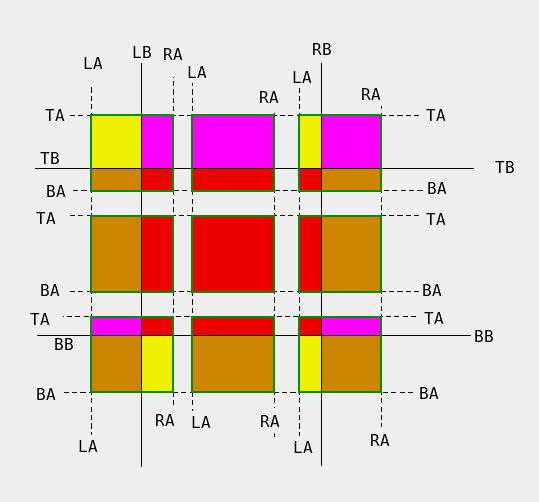
The OpenGL area is in the center, the black rectangle. The smaller rectangles are the event rectangles. Red areas should be drawn using OpenGL functions and the rest are copied from a bitmap.

This example assumes that the event rectangle (A) is smaller than the OpenGL rectangle (B), but my technique works in other cases as well. So, the problem is to find A-B, sometimes just one rectangle, sometimes four.

My observation is that, if an edge of B cuts thru A, then we have a difference rectangle on that side. For instance, if the left side of B cuts thru A, then the whole portion of A to the left of B is part of A-B.

When we do this, we can make A smaller and cut it by the edge in question. After all, we have already added the necessary part to the difference set. Here is some pseudo-code:

subtract_rectangle(A,B)

  result= empty
  if top(B) in [top(A)..bot(A)] 
    result= result + rectangle{ left(A), top(A), right(A), top(B) }
    top(A)= top(B)
  end

  if bot(B) in [top(A)..bot(A)]
    result= result + rectangle{ left(A), bot(B), right(A), bot(A) }
    bot(A)= bot(B)
  end

  if left(B) in [left(A)..right(A)]
    result= result + rectangle{ left(A), top(A), left(B), bot(A) }
    left(A)= left(B)
  end

  if right(B) in [left(A)..right(A)]
    result= result + rectangle{ right(B), top(A), right(A), bot(A) }
    right(A)= right(B)
  end

The nice thing is, if A and B intersect at all, by the end of this function A contains the intersection.