Karatsuba Algorithm for Multiplication

Multiplication of long numbers is usually done by representing each number with a polynomial and then using polynomial multiplication algorithms on those.

Let's assume we want to multiply two numbers A and B. We can group the digits of each number by M digits per group.

 A= a₂ : a₁ : a₀,      a₁ and a₀ have M digits
 B= b₂ : b₁ : b₀,      b₁ and b₀ have M digits

If the numbers are expressed in base D, then we can rewrite them as sums. In most academic discussions D is taken as 2, but it's more practical to use D=2^W where W is the width of a machine word.

 A= a₂D^2M + a₁D^M+a₀
 B= b₂D^2M + b₁D^M+b₀

These can be thought of as values of P(x) and Q(x) at the point x=D^M.

 P(x)= a₂x²+a₁x+a₀
 Q(x)= b₂x²+b₁x+b₀

Now consider the polynomial R(x)

 R(x)=P(x)Q(x)

If the coefficients of R(x) can be computed efficiently, then we have an algorithm to efficiently compute AB=R(D^M).

This is the basis of many Karatsuba-like algorithms regarding multiplication. It's a well-studied field, with a known O(Nlog(N)) algorithm for input size N. However, most algorithms do not payoff for numbers that are suitable for current hardware in 2021.

The Karatsuba algorithm isn't very complex. Therefore, its complexity doesn't cost too much even for smaller numbers with 300 digits or so. Therefore, I'm going to explore it in these pages.

The algorithm represents A and B with linear polynomials P(x) and Q(x):

 A= a₁:a₀= a₁D^M+a₀
 B= b₁:b₀= b₁D^M+b₀

 P(x)=a₁x+a₀
 Q(x)=b₁x+b₀

 R(x)=P(x)Q(x)= a₁b₁x²+(a₀b₁+a₁b₀)x+a₀b₀

We have three coefficients z₀, z₁ and z₂.

 R(x)=P(x)Q(x)= z₂x²+z₁x+z₀
 z₂= a₁b₁
 z₁= a₀b₁+a₁b₀
 z₀= a₀b₀

If we do it the simple way, then we have to do four multiplications. However, we can compute z₁ in terms of z₀ and z₂. This lets us reduce the number of multiplications to three.

 z₁= a₀b₁+a₁b₀
 z₁= (a₀-a₁)(b₁-b₀)+z₂+z₀

+z₂ cancels out the -a₁b₁ term, and +z₀ cancels out the -a₀b₀ term, leaving z₁ with the original value. This results in N^log₂3 multiplications instead of N². This is also the complexity of the overall algorithm, Θ(N^log₂3).

Representation of Big Numbers

Each number will be a string of WORDs. A WORD is the biggest machine word on which the CPU can make multiplications without losing the upper half. For x86, maximum register size is usable for this purpose because it has an unsigned multiplication instruction which produces a result twice as large as a register. For other architectures that don't have this, half the maximum register size must be used.

I will store numbers in little-endian order of words. Most operations proceed from least significant words to most significant. Even though it's more convenient to proceed from higher addresses to lower addresses, it gets confusing quite quickly. Therefore, I will use little-endian for now.

A number will be a simple struct, since they never change size:

typedef struct
{
  int length;
  WORD *lsw;
} BN;

X86 Considerations

The following instructions are available for unsigned multiplication:

mul : multiplies two 64-bit values. One of the multiplicands must reside in RAX. The 128-bit result is stored in RDX:RAX. This basic instruction is available on all 64-bit CPUs.
VPMULUDQ: uses SSE2 registers, doing four simultaneous 32-bit multiplications resulting in four 64-bit values. This is only possible if the CPU has 256-bit SSE2 registers. This extension is called AVX. Without it, SSE2 has 128 bit registers.
mulx: uses regular registers like mul. The implicit operand is in RDX and the destination registers are flexible. This is available only if the CPU has the BMI2 extension. This instruction doesn't affect flags.

Of the three, mulx is the best choice but it isn't available everywhere. This is true of older CPUs and maybe low-end CPUs like those found in tablets etc. I will use mul initially. Later on, I can use mulx if I can demonstrate a significant performance improvement.

The second choice results in the same number of multiplications as the first, but we still need to combine the resulting four 64-bit values into two 64-bit values. Also, there is some extra setup for this to work. Therefore, it's not a very good choice.

Implementing Karatsuba Algorithm Properly

The Karatsuba algorithm is specified for numbers that have the same number of digits. For other cases, most people simply pad the numbers to equal length or even to a power of two length. This is not optimal behaviour in terms of speed. Below is the code specified by most people on tutorials. ⊗ is Karatsuba multiplication and × is simple multiplication. × is sometimes called high-school or third grader multiplication.

 A ⊗ B is
   if |A|=1 or |B|=1
      return A × B

   M= ⌊min(|A|,|B|)/2⌋
   split A -> a1:a0  (a0, b0 have M digits)
   split B -> b1:b0  

   z0= a0 ⊗ b0
   z2= a1 ⊗ b1
   z1= (a0-a1)⊗(b1-b0) + z0 + z2

   return z2<<2M + z1<<M + z0

The problem here is the computation of M: the number of digits for the next iteration. When the lengths of A and B differ, the choice made here makes it even bigger in the next round. This continues until the ratio of their lengths become so high that the algorithm basically deteriorates towards × operation.

I thought of switching to × operator when this ratio becomes too high, using the following code:

 A ⊗ B is
   if |A| < |B|  ⇒ A ⟷ B
   if |B|=1      ⇒ return A × B

   if |A| ≥ FACTOR*|B|
      split A -> a1:a0     (a0 has N=⌊|A|/2⌋ digits)
      return (a1 ⊗ B)<<N + (a0 ⊗ B)

   M= ⌊|B|/2⌋
   split A -> a1:a0  (a0, b0 have M digits)
   split B -> b1:b0  

   z0= a0 ⊗ b0
   z2= a1 ⊗ b1
   z1= (a0-a1)⊗(b1-b0) + z0 + z2

   return z2<<2M + z1<<M + z0

This turned out to be quite a bit better, but not still that good. Finally, I arrived at the correct way of implementing this. Instead of decreasing the length of numbers by a small amount at each recursive call, decreasing them with the biggest reasonable number works much better.

 A ⊗ B is
   if |A| < |B|  ⇒ A ⟷ B
   if |B|=1      ⇒ return A × B

   M= ⌊|A|/2⌋
   split A -> a1:a0       (a0 has M digits)

   if M ≥ |B|
     return (a1 ⊗ B)<<M + (a0 ⊗ B)

   split B -> b1: b0      (b0 has M digits) 
   z0= a0 ⊗ b0
   z2= a1 ⊗ b1
   z1= (a0-a1)⊗(b1-b0) + z0 + z2

   return z2<<2M + z1<<M + z0

Here is a plot of the number of multiplications done by the three algorithms. One of the arguments is fixed at 4096 digits. The X axis shows the length of the other argument.

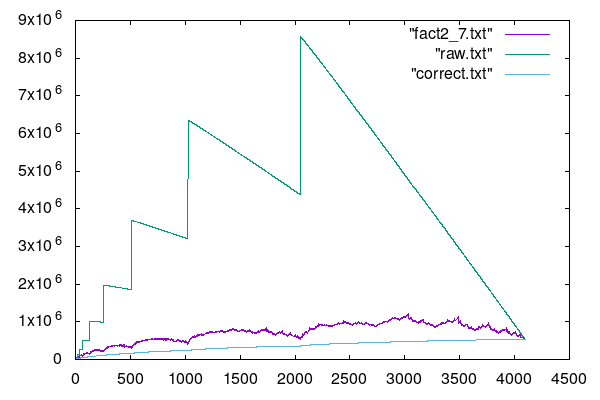
The factor 2.7 performs the best for the second algorithm, but it's still worse than the "correct" version.

Is Karatsuba Worth It?

For a 2048 bit prime, we will have 32 words with 64-bits per word. Simple multiplication requires 32*32=1024 word multiplications. Karatsuba algorithm does this with 243 word multiplications. There is a saving of 77%, but it's only 781 multiplication instructions. The complexity of the ⊗ causes many more instructions to be executed, a lot of them being jumps and memory allocations.

For relatively small primes like 2048 bits, ⊗ can outperform × only if it's written in the most efficient way possible. This version should contain a minimum number of conditionals and recursive calls. It should probably be optimized to run only for a certain size of integer. I can predetermine where each value goes and only perform arithmetic instructions at run time. It's OK if I just use × for smaller integers like this, but I'm just curious.

Before I go into more detail, let's look at a few problems with the algorithm.

Hairy Bits

The final algorithm computes z1 based on z0 and z2, as well as the product of two differences. Let's remember:

   z1= (a0-a1)⊗(b1-b0) + z0 + z2

Here, (a0-a1) and (b1-b0) can generate negative numbers. Handling negative numbers can be done only by a separate sign bit since our numbers don't have a fixed number of bits. Also, we need to be able to handle big unsigned numbers. Therefore, twos complement can't be used and a magnitude-sign format is mandatory. However, the sign bit will mess up multiplications. The only option here is to store the sign of the difference as a flag apart from the rest of the data. So, the relevant part of the algorithm will look like:

  T_a = a0-a1 and S_a=  1, if a0 ≥ a1
  T_a = a1-a0 and S_a= -1, if a0 < a1
  T_b = b1-b0 and S_b=  1, if b1 ≥ b0
  T_b = b0-b1 and S_b= -1, if b1 < b0

  T= T_a⊗T_b
  z1= z2+z0 + T   ,  if S_a=S_b
  z1= z2+z0 - T   ,  if S_a≠S_b

We can simplify the notation above by defining two new operators:

A ⊖ B computes |A-B| along with the sign of A-B, returns these as two separate values.
A ⊕ B computes A+B if the sign associated with B is positive. It computes A-B otherwise.

So, the above code becomes simpler.

  [S_a, T_a]= a0 ⊖ a1
  [S_b, T_b]= b1 ⊖ b0
  S=  1,  if S_a = S_b
     -1,  otherwise
  z= z2 + z0 ⊕ [S,T_a ⊗ T_b]

If we use the values {0,1} instead of {-1,1} for S_*, then the conditional for the final S becomes an XOR operation.

The other solution to this is to use the formula:

  z1= (a0+a1)⊗(b0+b1) - z0 -z2

However, the terms here now generate a carry and thus grow the size of the subproblem by one. This is worse than the other option because we can't predetermine the storage, it will depend on the actual run-time values for A and B. If we simply allocate an extra space for the carry all the time, then the algorithm becomes much less efficient. Here is the corresponding plot:

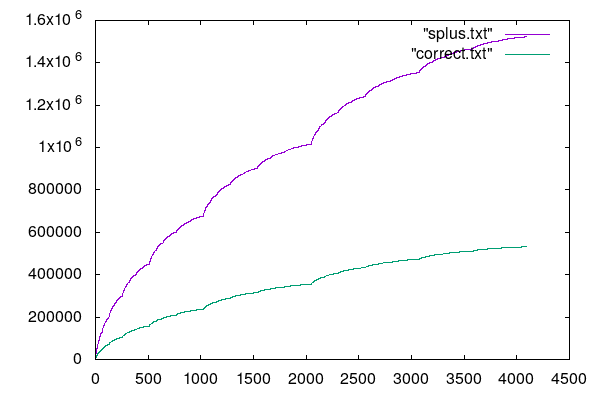
Allocating Space Efficiently

Well, doing pre-determined location/code seems to be a little out of my league for now. Maybe later I can do it. Instead of that, I will use the fact that results and other temporary variables are allocated in an orderly manner, just like a stack. I could determine the necessary size of the stack beforehand, allocate the space and then use it without paying too much for allocation/deallocation. Reducing memory footprint will also improve cache performance.

Let's write down the final version of our function and optimize it to use pre-allocated space.

 A ⊗ B is
   if |A| < |B|  ⇒ A ⟷ B
   if |B|=1      ⇒ return A × B
   M= ⌊|A|/2⌋
   a1:a0 = A    s.t. |a1|= |A|-M, |a0|= M
   if M ≥ |B|    ⇒ return (a1 ⊗ B)<<M + (a0 ⊗ B)
   b1:b0 = B    s.t. |b1|= |B|-M, |b0|= M
   z0= a0 ⊗ b0
   z2= a1 ⊗ b1
   <S_a,T_a> = a0 ⊖ a1
   <S_b,T_b> = b1 ⊖ b0
   z1= z0 + z2 ⊕ <S_a XOR S_b,T_a ⊗ T_b>
   return z2<<2M + z1<<M + z0

Now, let's define some operators to deal with memory operations rather than abstract numbers. I will write this algorithm for a little-endian storage scheme. The least significant digit of a number will have the index 0. X{K} indicates substring of X, starting with digit K.

T((X)) indicates a temporary variable of size X, allocated at the point where this expression occurs.

 R= A ⊗ B is      // R initially all zeros
  1:   if |A| < |B|  ⇒ A ⟷ B
  2:   if |B|=1      ⇒ R= A × B  .done.
  3:   M= ⌊|A|/2⌋
  4:   a1:a0 = A    s.t. |a1|= |A|-M, |a0|= M
  5:   if M ≥ |B| 
  6:      R = a0 ⊗ B
  7:      T((|a1|+|B|)) = a1 ⊗ B
  8:      R{M} += T
  9:      .done.
 10:   b1:b0 = B    s.t. |b1|= |B|-M, |b0|= M 
 11:   z0((|a0|+|b0|))= a0 ⊗ b0
 12:   z2((|a1|+|b1|))= a1 ⊗ b1
 13:   S_a,T_a = a0 ⊖ a1
 14:   S_b,T_b = b1 ⊖ b0
 15:   P((|T_a|+|T_b|))= T_a ⊗ T_b
 16:   z1((max(|P|,|z0|,|z2|)+1))  // initialized to all zeros
 17:   z1 += z0
 18:   z1 += z2 
 19:   z1 ⊕= <S_a XOR S_b, P>
 20:   R+= z0
 21:   R{2M}+= z2
 22:   R{M} += z1

Let's analyse the last three lines. Until (20), there is no update to R since the beginning, where it was assumed to be filled with zeros. Length of z0 is 2*M. Therefore, (20) can be replaced by

20A: R[0..2M-1]= z0

A similar argument applies to (21), since the above statement didn't touch R{2M} (it stopped one short).

21A: R{2M}= z2

Now let's expand (22) with the value of z1:

22A: R{M}+= z0 + z2 ⊕ <S_a XOR S_b, P>
          separating into individual components:
22A1: R{M} += z0
22A2: R{M} += z2
22A3: R{M} ⊕=  <S_a XOR S_b, P>

If we have allocated space for z0, z2 and P, then we don't need to allocate space for z1 because its value is used only once and replacing it with its value works just as well. In computation of z1, we make two 2M-digit additions. We do another one while adding z1 to R, totalling to three 2M-digit additions. In (22A1..22A3), we also have three 2M-digit additions. Therefore, storing z1 somewhere else and then adding to R doesn't have any advantages.

This lets us remove lines (16..19) from the code, given that we replace (22) by (22A1..22A3). Let's analyse the latter. Before entering 22A1, we have the following in R:

     MSW                             LSW
 R=   [UUUuuuuuuuuuuYYYYYYYYYYyyyyyyyyyy]
          ^         ^         ^
          |         |         |
       index 3M-1   |      index M-1
                index 2M-1
  Y/y: digits of z0
  U/u: digits of z2

We know that we have M digits of u and at least one digit of U as follows:

  |R|= |A| + |B|
  |A|= |a0| + |a1|
  |B|= |b0| + |b1|
  |R|= |a0| + |b0| + |a1| + |b1|
  |R|= 2M + |a1| + |b1|     (a0,b0 are lower M digits of A and B)

  M= ⌊|A|/2⌋
  M ≤ |A|/2 < M+1
  -M ≥ -|A|/2             (multiply by -1, use only left ineq.)
  |A|-M ≥ |A|-|A|/2       (add |A| everywhere)
  |A|-M ≥ |A|/2
  |a1|= |A|-M             (from splitting)
  |a1| ≥ |A|/2 ≥ M        (from the top)

  |B| > M                 ( from (5) )
  |B| - M > 0             (subtract M from both sides)
  |b1|= |B| - M           (from splitting)
  |b1| > 0             
  |b1| ≥ 1                (|b1| is an integer)
  
  |a1| + |b1| ≥ M + 1

When we do (22A1) and (22A2), we're adding the following numbers:

     R=   [UUUuuuuuuuuuuYYYYYYYYYYyyyyyyyyyy]
 z0<<M=   [   YYYYYYYYYYyyyyyyyyyy          ]  //spaces are 0s
 z2<<M=   [          UUUuuuuuuuuuu          ]

If we can do this addition using only the initial value of R (which was composed of z0 and z2), then we don't need to allocate space for z0 and z2 at all. They can be computed directly into the appropriate places in R, and then we would use only R to add their values to R{M}. Hence, no variables needed for z0 and z2. I think this can be done with a fancy addition operator.

If we do this with a normal addition, it doesn't work because when we do our very first addition (involving the rightmost Y,y, and u)

  R[M]= R[M] + R[0]+ R[2M]

  R[M]= Y₀ + y₀ + u₀

We're destroying R[M], which will be needed again later on, when calculating R[2M] (involving the rightmost u Y and U):

  R[2M]= R[2M] + R[M]+ R[3M]   // will not work!

  R[2M]= u₀ + Y₀ + U₀

In both of these, there is a common addend u₀ + Y₀. If I can exploit that, I might just get away with this. If I could sum

     R=   [UUUuuuuuuuuuuYYYYYYYYYYyyyyyyyyyy]
          [   YYYYYYYYYYuuuuuuuuuu          ] 
          [          UUUyyyyyyyyyy          ]

instead of the original, it would have the same value. My idea now is to do two additions at each iteration of the loop, updating both the upper and lower halves of R at once. At each iteration, a Y and u value would be read, then their sums would be added a y and a U value separately. The results would then be stored in the lower and upper halves of R.

The number of U terms is at least one, but it can also be higher than M. Remember that U/u terms come from z2, which is computed by a1⊗b1. So, |z2|=|a1|+|b1|. The maximum value for each of the terms on the right is M+1 (for |A|=|B|=2M+1). Therefore, M+1≤|z2|≤2M+2 which implies that 1≤|U|≤M+2. This implies that we can also encounter a situation like the following: (M=10, |U|=12)

     R=   [UUUUUUUUUUUUuuuuuuuuuuYYYYYYYYYYyyyyyyyyyy]
          [            YYYYYYYYYYuuuuuuuuuu          ] 
          [          UUUUUUUUUUUUyyyyyyyyyy          ]

When this happens, we need to add the lower words of U and higher words of U to form the sum, while also using the carry values from the previous two parallel sums. The maximum number of extra 'U' words is two, but the code should be general enough to facilitate testing.

Let's write some code so that we can argue better.

mixed_sum(R,M):
  carry_l= 0
  carry_h= 0
  for i = 0 .. M-1
    Y_i= R[M+i]
    u_i= R[2M+i]
    y_i= R[i]
    U_i= R[3M+i]
    carry_l:R[M+i]= Y_i+u_i+y_i+carry_l
    carry_h:R[2M+i]= Y_i+u_i+U_i+carry_h
  C= 0
  for i = 0 .. |R|-4M
    C:R[3M+i] = R[3M+i] + R[4M+i] + C
  propagate carry_l to R{2M}
  propagate carry_h to R{3M}
  propagate C to R{3M+i}

carry_h/carry_l should be at least 2 bits wide. If we add three arbitrary binary numbers, these can be as big as we want. Let's try all 1s.

              Y=    11111
              u=    11111
            sum=  1:11110
              U=    11111
            sum= 10:11101

With this method of summation, we can get rid of variables z0,z1 and z2. Now let's write the current algorithm with these modifications:

 R= A ⊗ B is      // R initially all zeros
  1:   if |A| < |B|  ⇒ A ⟷ B
  2:   if |B|=1      ⇒ R= A × B  .done.
  3:   M= ⌊|A|/2⌋
  4:   a1:a0 = A    s.t. |a1|= |A|-M, |a0|= M
  5:   if M ≥ |B| 
  6:      R = a0 ⊗ B
  7:      T((|a1|+|B|)) = a1 ⊗ B
  8:      R{M} += T
  9:      .done.
 10:   b1:b0 = B    s.t. |b1|= |B|-M, |b0|= M 
 11:   R= a0 ⊗ b0
 12:   R{2M}= a1 ⊗ b1
 13:   S_a,T_a = a0 ⊖ a1
 14:   S_b,T_b = b1 ⊖ b0
 15:   P((|T_a|+|T_b|))= T_a ⊗ T_b
 16:   mixed_sum(R, M) 
 17:   R{M} ⊕= S_a XOR S_b : P

The memory requirement is calculated here. Up to input sizes of 64K digits (4096Kbits for 64-bit words), 4|A|+60 words of memory is enough for temporary variables in addition to the |A|+|B| sized product.

The total memory requirement is therefore 5|A|+|B|+60.

Basic operations for this algorithm are explained here.

Performance Measurement

The following tests were done on a 2021 Intel Core i5-10200H processor, with 8MB cache and 4 cores, supporting 8 threads.

Each algorithm was run a multiple number of times and the total user-time was recorded using the Unix 'time' tool. At each run, two random numbers were read from /dev/urandom. The sizes of the numbers are chosen randomly to be between [MAXSIZE/2,MAXSIZE] bytes. In the graphs below, the total time vs. MAXSIZE is plotted.

The first one is about long numbers. Each algorithm was run 1K times.

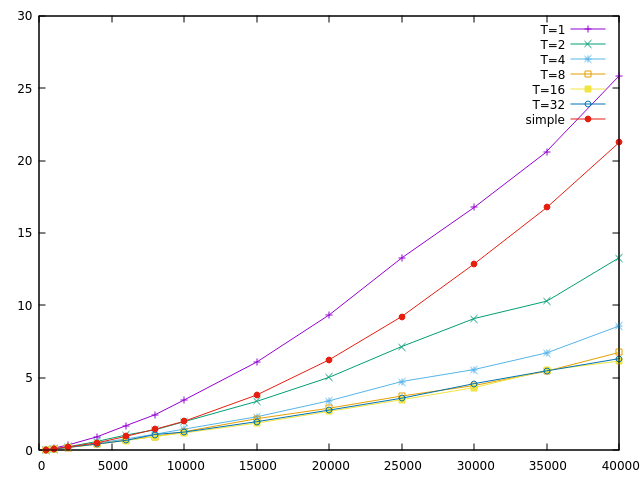
In the algorithm I have shown above, we revert to × operator when |B|=1. This is not optimal since doing all that setup and jumps just to avoid doing a couple of extra multiplications doesn't pay off. This is clearly shown in the plot T=1. Each of the plots correspond to an algorithm where the switchover is done such that:

  if |B|≤T return A × B;

As expected, T=1 performs worse than simple multiplication. T=2 seems to be OK but the best performance is achieved with T=8 or greater.

Here is the second measurement. Here, each algorithm was run 10K times.

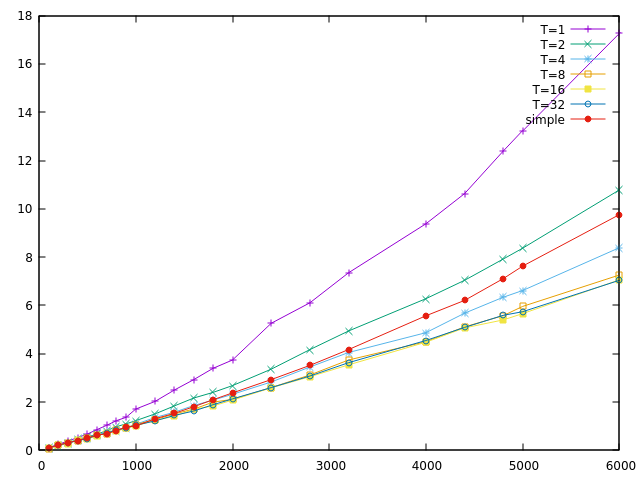
T=32 seems to be the best option overall, providing good performance for both long and short inputs. However, T=8 isn't that different and might even be better for processors that don't have as many ALUs.

In any case, the first perceptible difference between simple multiplication and the Karatsuba algorithm happens around MAXSIZE=1600. This corresponds to about 200 digits for a machine with 64-bit words. The expected size using random length selection is 100+50=150. In theory, we could increase T up to 150 and still have the same performance, with less memory usage (and corresponding cache misses).

Let's try that and see what happens. Let's compare T=32 vs. T=150.

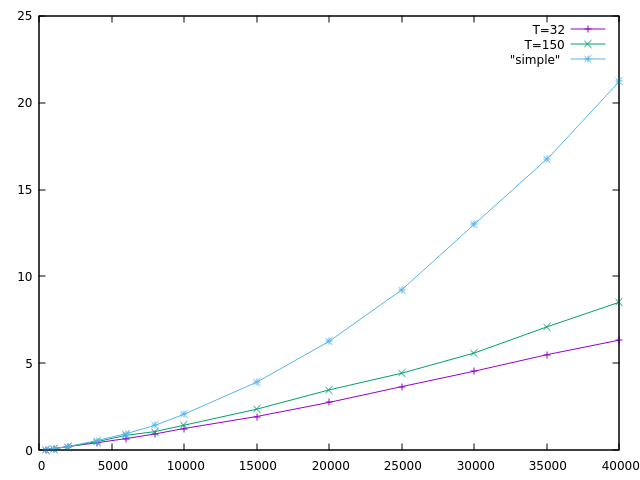
We see that T=150 is worse than T=32. There is probably some optimal value between the two but I'm already content with T=8. The memory usage difference between T=32 and T=150 isn't that much either. I should have foreseen this because most of the memory allocated at the leaf nodes of the algorithm is reused immediately. Here is a simple calculation of memory requirements for 1000 digits.

kspace[1](1000,1000)= 4004                                                      
kspace[32](1000,1000)= 3880                                                     
kspace[150](1000,1000)= 3500

A Possible Improvement

In my implementation, memory allocation is done on a pre-allocated stack but each chunk is zeroed-out before use. This is because my × operator is similar to a mul-add function. The result array is therefore assumed to be filled with zeros.

This can be remedied by dividing the × operator into two. The first step will initialize the first |A|+1 words of the output array. After that the remaining part will run normally. This is further discussed in the basic operations page.

The algorithm which doesn't need initialized storage is called "malloc" below. The regular one is called "calloc". You can see that it's slightly faster overall.

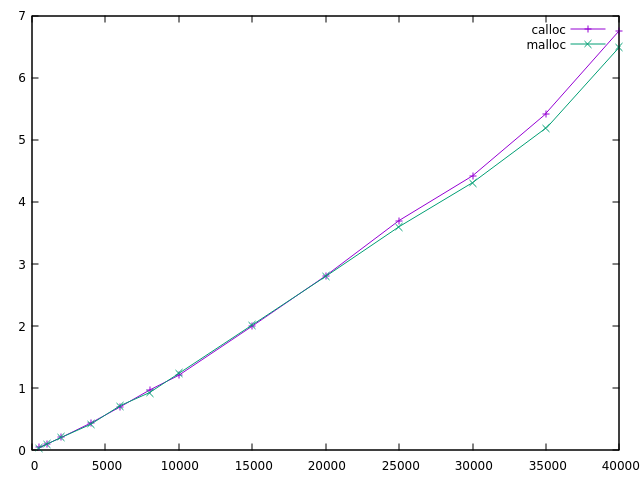
I think this difference could be bigger for machines with less cache. Also, it's more convenient to simply allocate one temporary space and then re-use it without further initialization for multiple operations.

Source Code

You may access the source code from here. This is the latest version which uses uninitialized arrays for both output and temporary space.